
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 476 Атанасян — Подробные Ответы
Докажите, что площадь ромба равна половине произведения его диагоналей. Вычислите площадь ромба, если его диагонали равны:
а) 3,2 дм и 14 см;
б) 4,6 дм и 2 дм.
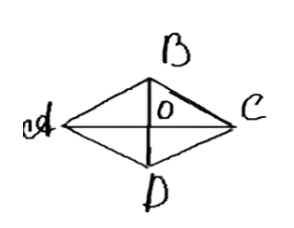
Дано: ABCD — ромб.
а) AC = 14 см, BD = 32 см;
б) AC = 2 дм, BD = 4,6 дм.
Требуется доказать:
S_ABCD = (BD * AC) / 2
Решение:
1. Диагонали ромба пересекаются под прямым углом и делятся пополам.
2. Ромб состоит из четырех равных прямоугольных треугольников: AOD, DOC, AOB, BOC.
3. Площадь одного треугольника: S_AOD = (1/2) * AO * OD.
4. AO = AC / 2, OD = BD / 2. Подставим:
S_AOD = (1/2) * (AC / 2) * (BD / 2) = (AC * BD) / 8.
5. Площадь ромба: S_ABCD = 4 * S_AOD = 4 * (AC * BD) / 8 = (AC * BD) / 2.
Подставим значения:
а) S_ABCD = (32 * 14) / 2 = 224 см².
б) S_ABCD = (4,6 * 2) / 2 = 4,6 дм².
Ответ:
а) 224 см²;
б) 4,6 дм².
Дано: ABCD — ромб.
а) AC = 14 см, BD = 32 см;
б) AC = 2 дм, BD = 4,6 дм.
Требуется доказать, что площадь ромба вычисляется по формуле:
S_ABCD = (BD * AC) / 2
Решение:
1. Диагонали ромба пересекаются под прямым углом и делятся пополам. Это свойство ромба, которое следует из его определения. Пусть точка пересечения диагоналей — точка O. Тогда AO = OC = AC / 2, BO = OD = BD / 2.
2. Диагонали делят ромб на четыре равных прямоугольных треугольника: AOD, DOC, AOB, BOC.
3. Рассмотрим один из треугольников, например, AOD. Его площадь можно найти по формуле площади прямоугольного треугольника:
S_AOD = (1/2) * AO * OD
4. Подставим выражения для AO и OD через длины диагоналей ромба: AO = AC / 2, OD = BD / 2. Тогда:
S_AOD = (1/2) * (AC / 2) * (BD / 2) = (AC * BD) / 8
5. Площадь ромба складывается из площади четырех таких треугольников:
S_ABCD = 4 * S_AOD = 4 * (AC * BD) / 8 = (AC * BD) / 2
Таким образом, формула площади ромба доказана:
S_ABCD = (BD * AC) / 2
Теперь найдем площадь ромба для каждого случая:
а) Если AC = 14 см, BD = 32 см:
S_ABCD = (32 * 14) / 2 = 448 / 2 = 224 см²
б) Если AC = 2 дм, BD = 4,6 дм:
S_ABCD = (4,6 * 2) / 2 = 9,2 / 2 = 4,6 дм²
Ответ:
а) Площадь ромба равна 224 см²
б) Площадь ромба равна 4,6 дм²
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!