ГДЗ по Геометрии 8 класс Номер 475 Атанасян — Подробные Ответы

Начертите треугольник ABC. Через вершину A проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.

1. Построим треугольник ABC. Его площадь вычисляется по формуле:
\[ S_{ABC} = \frac{1}{2} \cdot h \cdot BC \]

2. Разделим сторону BC на три равные части: \( BD = DE = EC \).

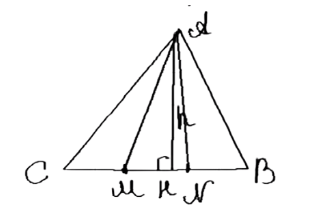
3. Проведем прямые из вершины A через точки D и E. Эти прямые разделят треугольник ABC на три треугольника: ABD, ADE и AEC.

4. Поскольку основания \( BD, DE, EC \) равны, а высота из вершины A одинакова для всех трех треугольников, их площади равны:
\[ S_{ABD} = S_{ADE} = S_{AEC} = \frac{1}{2} \cdot AE \cdot BD \]

Таким образом, треугольник ABC разделен на три равных по площади треугольника.

1. Построим произвольный треугольник ABC. Его площадь можно вычислить по формуле:
S_ABC = (1/2) * h * BC,
где BC — основание треугольника, а h — высота, опущенная из вершины A на сторону BC.

2. Чтобы разделить треугольник ABC на три равных по площади треугольника, нужно отметить точки D и E на основании BC так, чтобы отрезки BD, DE и EC были равны. То есть:
BD = DE = EC.
Таким образом, сторона BC делится на три равные части.

3. Через вершину A проведем прямые линии, проходящие через точки D и E. Эти прямые пересекут треугольник ABC, разделив его на три меньших треугольника: ABD, ADE и AEC.

4. Рассмотрим площадь каждого из этих треугольников. Основания BD, DE и EC равны между собой по построению. Высота для каждого из треугольников одинакова, так как она совпадает с высотой треугольника ABC, опущенной из вершины A на прямую BC.

5. Площадь каждого из треугольников можно выразить как:
S_ABD = S_ADE = S_AEC = (1/2) * AE * BD.

6. Таким образом, треугольник ABC разделен на три равных по площади треугольника.