Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 474 Атанасян — Подробные Ответы
Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой.
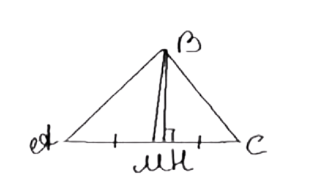
Дано: треугольник ABC, BM – медиана. Нужно сравнить площади треугольников ABM и MBC.
Решение:
1. Проведем высоту BH:
BH – это высота в треугольнике ABM к стороне AM и одновременно высота в треугольнике MBC к стороне MC.
2. Площадь треугольника ABM:
\[ S_{ABM} = \frac{1}{2} \cdot AM \cdot BH \]
3. Площадь треугольника MBC:
\[ S_{MBC} = \frac{1}{2} \cdot MC \cdot BH \]
4. Так как BM – медиана, то AM = MC.
5. Подставим AM = MC:
\[ S_{ABM} = S_{MBC} \]
Ответ: \[ S_{ABM} = S_{MBC} \]
Дано: треугольник ABC, BM – медиана. Необходимо сравнить площади треугольников ABM и MBC.
Решение:
1. Рассмотрим треугольники ABM и MBC. Площадь каждого из них вычисляется по формуле площади треугольника: площадь равна половине произведения основания на высоту.
2. Проведем высоту BH из вершины B. Эта высота является общей для обоих треугольников, так как она перпендикулярна стороне AC, которая разделена медианой BM на два равных отрезка AM и MC.
3. Для треугольника ABM основанием является отрезок AM, а высотой – BH. Площадь треугольника ABM равна:
S_ABM = 1/2 * AM * BH.
4. Для треугольника MBC основанием является отрезок MC, а высотой – BH. Площадь треугольника MBC равна:
S_MBC = 1/2 * MC * BH.
5. Так как BM – медиана, то по определению медианы отрезки AM и MC равны. Следовательно, AM = MC.
6. Подставляя равенство AM = MC в формулы для площадей, получаем:
S_ABM = 1/2 * AM * BH,
S_MBC = 1/2 * AM * BH.
7. Таким образом, S_ABM = S_MBC.
Вывод: площади треугольников ABM и MBC равны. Ответ: S_ABM = S_MBC.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.