ГДЗ по Геометрии 8 класс Номер 467 Атанасян — Подробные Ответы

Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур

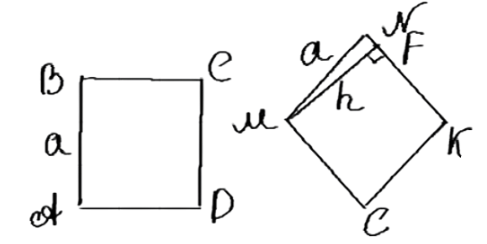
Дано: ABCD — квадрат, EFMN — ромб. Нужно сравнить площади S_ABCD и S_EFNM.

Решение:

1. Площадь квадрата:
S_ABCD = AB^2

2. Площадь ромба:
S_EFNM = MN * EH / 2

3. Периметры квадрата и ромба равны:
P_ABCD = 4 * AB
P_EFNM = 4 * EM
Так как AB = EM, то стороны квадрата и ромба равны.

4. В треугольнике ENM диагональ EM — гипотенуза, а EH — катет. Следовательно, EM > EH.

5. Умножаем обе части неравенства на MN:
EM * MN > EH * MN

6. Таким образом:
EM^2 > EM * EH

7. Площадь квадрата:
S_ABCD = EM^2

8. Площадь ромба:
S_EFNM = MN * EH / 2

Так как EM^2 > EM * EH, то S_ABCD > S_EFNM.

Ответ: S_ABCD > S_EFNM.

Дано: ABCD — квадрат, EFMN — ромб. Необходимо сравнить площади S_ABCD и S_EFNM.

Решение:

1. Площадь квадрата вычисляется через квадрат длины его стороны:
S_ABCD = AB^2

2. Площадь ромба определяется как половина произведения его диагоналей:
S_EFNM = (MN * EH) / 2

3. Периметр квадрата равен:
P_ABCD = 4 * AB

Периметр ромба равен:
P_EFNM = FE + FN + NM + EM = 4 * EM

Так как сторона квадрата AB равна стороне ромба EM, получаем:
AB = EM

4. Рассмотрим треугольник ENM, образованный диагоналями ромба. В этом треугольнике диагональ EM — гипотенуза, а диагональ EH — катет. Из свойств прямоугольного треугольника следует, что гипотенуза всегда больше любого из катетов:
EM > EH

5. Умножим обе части неравенства EM > EH на диагональ MN (MN > 0):
EM * MN > EH * MN

6. Выразим площади через найденные соотношения. Площадь квадрата:
S_ABCD = EM^2

Площадь ромба:
S_EFNM = (MN * EH) / 2

7. Из неравенства EM^2 > EM * EH следует, что площадь квадрата больше площади ромба:
S_ABCD > S_EFNM

Ответ: S_ABCD > S_EFNM.