
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 465 Атанасян — Подробные Ответы
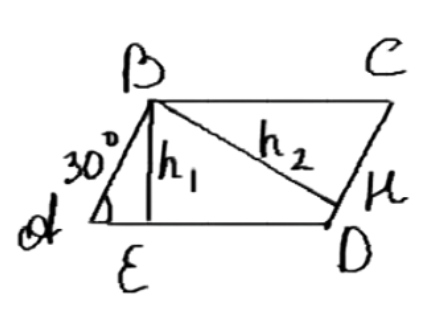
Острый угол параллелограмма равен 30°, а высоты, проведённые из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.
Дано: ABCD — параллелограмм, ∠A = 30°, h1 = 2 см, h2 = 3 см. Найти площадь параллелограмма S.
Решение:
1. Из условия ∠A = 30° следует, что BE = 1/2 AB.
2. AB = 2 × BE = 2 × 2 = 4 см.
3. В параллелограмме AB = CD, значит CD = 4 см.
4. Площадь параллелограмма вычисляется как S = h2 × CD.
Подставляем: S = 3 × 4 = 12 см².
Ответ: 12 см².
Дано:
ABCD — параллелограмм, угол A равен 30°, высота h1 = 2 см, высота h2 = 3 см.
Найти: площадь параллелограмма S.
Решение:
1. Рассмотрим угол A, который равен 30°. Из геометрических свойств высота BE, опущенная на сторону AB, составляет половину длины стороны AB. Следовательно, BE = 1/2 AB.
2. Так как AB = 2 × BE, подставляем значение высоты BE:
AB = 2 × 2 = 4 см.
3. В параллелограмме противоположные стороны равны, поэтому AB = CD. Таким образом, CD = 4 см.
4. Площадь параллелограмма вычисляется как произведение высоты, проведенной к одной из сторон, на длину этой стороны. Используем формулу для стороны CD:
S = h2 × CD.
5. Подставляем значения:
S = 3 × 4 = 12 см².
Ответ: 12 см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!