ГДЗ по Геометрии 8 класс Номер 463 Атанасян — Подробные Ответы

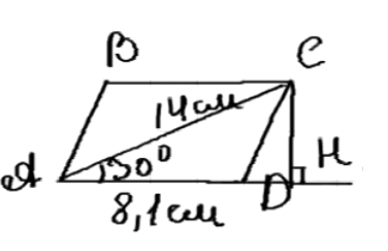
Сторона параллелограмма равна 8,1 см, а диагональ, равная 14 см, образует с ней угол в 30°. Найдите площадь параллелограмма. 

Дано: ABCD — параллелограмм, AD = 8,1 см, AC = 14 см, угол ∠CAD = 30°. Найти площадь параллелограмма.

Решение:

1. Проведем высоту \( CH \), перпендикулярную стороне \( AD \). Высота \( CH \) равна катету напротив угла \( 30^\circ \) в треугольнике \( ACH \), где гипотенуза \( AC = 14 \, \text{см} \). По свойству прямоугольного треугольника:
\(
CH = \frac{1}{2} \cdot AC = \frac{1}{2} \cdot 14 = 7 \, \text{см}
\)

2. Площадь параллелограмма вычисляется по формуле:
\(
S_{ABCD} = AD \cdot CH
\)
Подставим значения:
\(
S_{ABCD} = 8,1 \cdot 7 = 56,7 \, \text{см}^2
\)

Ответ:
\(
S_{ABCD} = 56,7 \, \text{см}^2
\)

Дано:
ABCD — параллелограмм.
AD = 8,1 см, AC = 14 см, угол CAD = 30°.
Найти: площадь параллелограмма S_ABCD.

Решение:

1. Площадь параллелограмма можно найти по формуле:
S_ABCD = основание × высота.

В данном случае основанием является сторона AD, а высотой — перпендикуляр CH, опущенный из точки C на сторону AD.

2. Чтобы найти CH, используем треугольник ACH. Угол CAD равен 30°, а сторона AC — это гипотенуза треугольника ACH.

Согласно свойству прямоугольного треугольника, катет, лежащий напротив угла 30°, равен половине гипотенузы. Значит:
CH = 1/2 × AC.

3. Подставляем значение AC:
CH = 1/2 × 14 = 7 см.

4. Теперь находим площадь параллелограмма:
S_ABCD = AD × CH.

Подставляем значения:
S_ABCD = 8,1 × 7 = 56,7 см².

Ответ:
Площадь параллелограмма S_ABCD = 56,7 см².