ГДЗ по Геометрии 8 класс Номер 461 Атанасян — Подробные Ответы

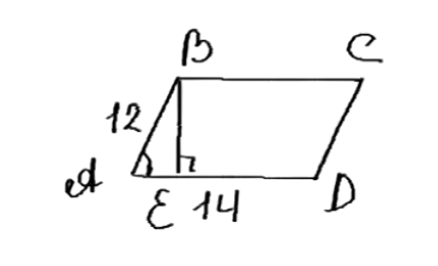
Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма. 

Дано: ABCD — параллелограмм, AB = 12 см, ∠BAD = 30°, BC = 14 см. Найти площадь S_ABCD.

Решение:
Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне. Проведём BH ⊥ AD. Треугольник ABH прямоугольный, ∠BAD = 30°. Катет BH, лежащий напротив угла 30°, равен половине гипотенузы AB:
BH = 1/2 * AB = 1/2 * 12 = 6 см.

Теперь площадь:
S_ABCD = BH * AD = 6 * 14 = 84 см².

Ответ: S_ABCD = 84 см².

Дано: ABCD — параллелограмм. Известно, что AB = 12 см, угол ∠BAD = 30°, BC = 14 см. Требуется найти площадь параллелограмма S_ABCD.

Решение:

Площадь параллелограмма вычисляется по формуле: S = основание * высота. В данном случае основанием является сторона AD, а высота — это перпендикуляр BH, опущенный из точки B на сторону AD.

1. Проведем высоту BH, которая перпендикулярна стороне AD. Рассмотрим прямоугольный треугольник ABH, в котором угол ∠BAD = 30°. Согласно свойству прямоугольного треугольника с углом 30°, катет, лежащий напротив этого угла (в данном случае BH), равен половине гипотенузы (в данном случае AB).

Вычислим длину высоты BH:
BH = 1/2 * AB
BH = 1/2 * 12 = 6 см.

2. Теперь найдем длину стороны AD. Так как ABCD — параллелограмм, противоположные стороны равны, следовательно, AD = BC = 14 см.

3. Найдем площадь параллелограмма, используя формулу:
S_ABCD = BH * AD
S_ABCD = 6 * 14 = 84 см².

Ответ: S_ABCD = 84 см².