
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 460 Атанасян — Подробные Ответы
Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.
Дан параллелограмм ABCD, у которого:
- BD — диагональ
- BD = 13 см
- BC = 12 см
Найти площадь параллелограмма SABCD.
Площадь параллелограмма равна произведению стороны и высоты, проведенной к этой стороне:
Подставляем значения:
Результат:
Ответ: SABCD = 156 см2
Дан параллелограмм ABCD, у которого:
- BD — диагональ
- BD = 13 см
- BC = 12 см
Найти площадь параллелограмма SABCD.
Решение:
Площадь параллелограмма равна произведению длины стороны и высоты, проведенной к этой стороне. В данном случае высота совпадает с длиной диагонали BD, так как диагональ перпендикулярна стороне BC.
Формула для площади параллелограмма:
Подставляем известные значения:
Выполняем умножение:
Ответ: SABCD = 156 см2.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


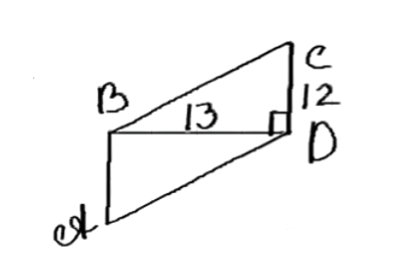

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!