
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 448 Атанасян — Подробные Ответы
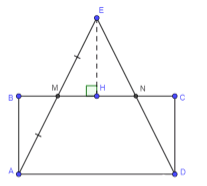
На стороне AD прямоугольника ABCD построен треугольник ADE так, что его стороны AE и DE пересекают отрезок BC в точках M и N, причём точка M — середина отрезка AE. Докажите, что S_ABCD = S_ADE.
Дано: ABCD — прямоугольник, AE и BC равны M, ED и AB равны N, AM = ME. Требуется доказать, что площадь прямоугольника ABCD равна площади треугольника ADE.
Рассмотрим доказательство. Проведем EN, перпендикулярный MN. Из условия AM = ME, углы BMA и EMH равны как вертикальные, поэтому треугольники ABM и EMH равны по гипотенузе и прилежащему углу. Следовательно, AB = EH. Так как AB = CD (стороны прямоугольника), то AB = EH = CD. Углы NEH и CDN равны как накрест лежащие, значит, треугольники AEHN и ADCN равны по катету и прилежащему углу.
Площадь треугольника ADE равна сумме площадей SAMND, SMEH и SEIN. Площадь прямоугольника ABCD равна сумме SAMND, SABM и SDCN. Так как треугольники ABM и EMH равны, их площади равны, а также равны площади треугольников AEHN и ADCN. Следовательно, площади ADE и ABCD равны.
Дано: ABCD — прямоугольник. AE и BC равны M, ED и AB равны N, AM = ME. Требуется доказать, что площадь прямоугольника ABCD равна площади треугольника ADE.
Рассмотрим доказательство.
Сначала проведем EN, перпендикулярный MN. Это позволяет разделить треугольник ADE на несколько частей: SAMND, SMEH и SEIN. Далее рассмотрим каждую часть.
По условию AM = ME. Углы BMA и EMH равны, так как они вертикальные. Следовательно, треугольники ABM и EMH равны по гипотенузе и прилежащему острому углу. Из равенства треугольников следует, что стороны AB и EH равны.
Так как ABCD — прямоугольник, то AB = CD. Следовательно, AB = EH = CD.
Углы NEH и CDN равны, так как они накрест лежащие. Следовательно, треугольники AEHN и ADCN равны по катету и прилежащему острому углу. Это означает, что их площади равны.
Теперь выразим площадь треугольника ADE как сумму площадей трех фигур: SAMND, SMEH и SEIN. То есть SADE = SAMND + SMEH + SEIN.
С другой стороны, площадь прямоугольника ABCD можно выразить как сумму площадей трех фигур: SAMND, SABM и SDCN. То есть S_ABCD = SAMND + SABM + SDCN.
Так как треугольники ABM и EMH равны, их площади равны, то есть SABM = SMEH. Аналогично, так как треугольники AEHN и ADCN равны, их площади также равны.
Подставим равенства в формулы. Получаем, что SAMND + SMEH + SEIN = SAMND + SABM + SDCN. Учитывая равенство площадей SMEH и SABM, а также равенство площадей AEHN и ADCN, заключаем, что SADE = S_ABCD.
Таким образом, доказано, что площадь прямоугольника ABCD равна площади треугольника ADE.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!