ГДЗ по Геометрии 8 класс Номер 446 Атанасян — Подробные Ответы

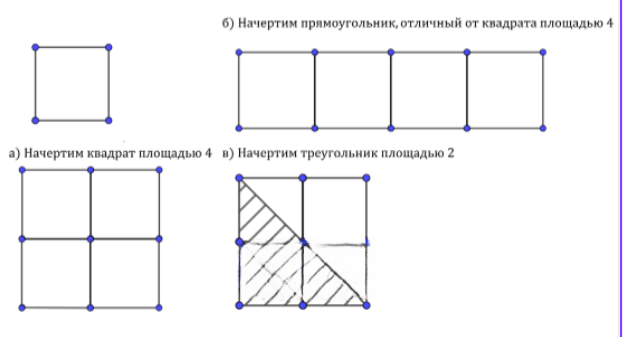
Начертите квадрат и примите его за единицу измерения площадей. Далее начертите: а) квадрат, площадь которого выражается числом 4; б) прямоугольник, отличный от квадрата, площадь которого выражается числом 4; в) треугольник, площадь которого выражается числом 2. 

Для квадрата с площадью 4 берем длину стороны 2, так как 2 × 2 = 4. Для прямоугольника берем стороны 1 и 4, так как 1 × 4 = 4. Для треугольника с площадью 2 берем основание 2 и высоту 2, так как (2 × 2) / 2 = 2.

Для решения задачи необходимо выполнить три построения: квадрат с площадью 4, прямоугольник с площадью 4, отличный от квадрата, и треугольник с площадью 2. Рассмотрим каждое из них подробно.

Сначала определим, что площадь квадрата вычисляется по формуле сторона умножить на сторону. Для квадрата с площадью 4 длина стороны должна быть равна 2, так как 2 умножить на 2 равно 4. Таким образом, строим квадрат со сторонами длиной 2 единицы.

Для построения прямоугольника с площадью 4, который отличается от квадрата, используем формулу площадь равна длина умножить на ширину. Выбираем длину равной 4 и ширину равной 1. Тогда площадь прямоугольника будет равна 4 умножить на 1, что дает 4. Строим прямоугольник с такими размерами.

Для построения треугольника с площадью 2 используем формулу площадь равна основание умножить на высоту и разделить на 2. Выбираем основание равным 2 и высоту равной 2. Подставляем в формулу: 2 умножить на 2 и разделить на 2 равно 2. Таким образом, строим треугольник с основанием 2 и высотой 2.

Все построения выполнены, площади фигур соответствуют заданным условиям.