ГДЗ по Геометрии 8 класс Номер 444 Атанасян — Подробные Ответы

 Докажите, что если фигура имеет две взаимно перпендикулярные оси симметрии, то точка их пересечения является центром симметрии фигуры.

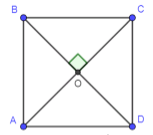
Дано: диагонали BD и AC пересекаются под прямым углом и являются осями симметрии.

Решение: так как BD и AC являются осями симметрии, каждая точка фигуры имеет симметричную относительно этих осей. Диагонали пересекаются в точке O и делятся пополам, то есть BO = OD и AO = OC. Следовательно, точка O равномерно делит фигуру и является центром симметрии.

Вывод: O — центр симметрии фигуры ABCD.

Дано: диагонали BD и AC пересекаются под прямым углом, являются осями симметрии четырехугольника ABCD. Точка O — точка пересечения диагоналей.

Требуется доказать, что точка O является центром симметрии четырехугольника ABCD.

Решение:

1. Рассмотрим свойства диагоналей BD и AC. Поскольку они являются осями симметрии, каждая точка фигуры имеет симметричную относительно этих осей. Это означает, что фигура симметрична относительно двух взаимно перпендикулярных осей.

2. Диагонали BD и AC пересекаются в точке O. По свойству диагоналей, которые являются осями симметрии, они делят друг друга пополам. Это означает, что отрезки BO и OD равны, а также отрезки AO и OC равны.

3. Центр симметрии — это точка, относительно которой любая точка фигуры имеет симметричную пару, причем расстояния от этой точки до пары точек равны.

4. Так как диагонали BD и AC делят друг друга пополам в точке O, она равномерно распределяет вершины фигуры ABCD. Это подтверждает, что точка O является точкой, относительно которой каждая точка фигуры имеет симметричную пару.

5. Таким образом, точка O обладает всеми свойствами центра симметрии: она находится на пересечении осей симметрии, делит диагонали пополам и обеспечивает равенство расстояний между симметричными точками фигуры.

Вывод: точка O является центром симметрии четырехугольника ABCD.