
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 443 Атанасян — Подробные Ответы
Сколько центров симметрии имеет пара параллельных прямых?
Даны две параллельные прямые a и b.
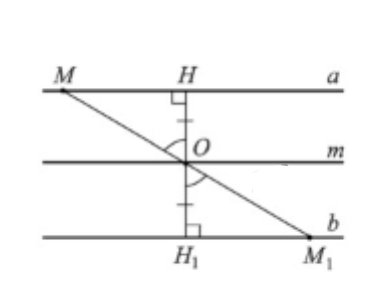
Проведем прямую t, которая параллельна a и b и находится на равных расстояниях от них. Выберем точку O на прямой t. Проведем через O перпендикуляр к прямым a и b, обозначив точки пересечения как H1 и H2. Так как t равноудалена от a и b, то OH1 = OH2, а значит, H1 и H2 симметричны относительно O.
Рассмотрим произвольную точку M на прямой a. Проведем прямую OM, которая пересечет b в точке M1. Треугольники OMH1 и OM1H2 равны, так как OH1 = OH2, угол при O общий, а также OM = OM1. Следовательно, M и M1 симметричны относительно O.
Таким образом, любая точка на прямой t является центром симметрии для данных параллельных прямых. Таких точек бесконечно много.
Рассмотрим две параллельные прямые a и b. Нам нужно доказать, что любая точка на прямой, равноудаленной от a и b, является центром симметрии этих прямых.
Сначала проведем прямую t, которая параллельна прямым a и b и находится на равных расстояниях от них. Прямая t делит расстояние между a и b пополам и называется серединной прямой. Теперь выберем произвольную точку O на прямой t и докажем, что она является центром симметрии для прямых a и b.
Проведем через точку O прямую, перпендикулярную к прямым a и b. Обозначим точки пересечения этой перпендикулярной с прямой a как H1, а с прямой b как H2. Так как прямая t равноудалена от a и b, то отрезки OH1 и OH2 равны. Это означает, что точки H1 и H2 симметричны относительно точки O.
Теперь рассмотрим произвольную точку M на прямой a. Проведем прямую через точки O и M. Эта прямая пересечет прямую b в некоторой точке M1. Нужно доказать, что точки M и M1 симметричны относительно точки O.
Рассмотрим треугольники OMH1 и OM1H2. У них общая сторона OM, углы при вершине O равны, так как они вертикальные, а отрезки OH1 и OH2 равны по построению. Следовательно, треугольники OMH1 и OM1H2 равны по двум сторонам и углу между ними. Из равенства треугольников следует, что OM равно OM1, а значит, точки M и M1 симметричны относительно точки O.
Таким образом, для любой точки M на прямой a существует точка M1 на прямой b, симметричная ей относительно точки O. Это справедливо для любой точки O на прямой t, поскольку прямая t является геометрическим местом точек, равноудаленных от a и b.
Следовательно, любая точка на прямой t является центром симметрии для данных параллельных прямых a и b.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!