Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 442 Атанасян — Подробные Ответы
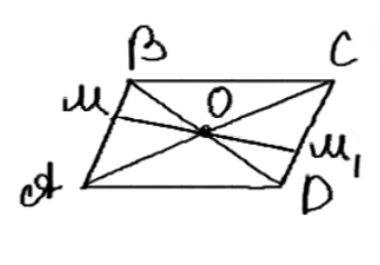
Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.
Дано: ABCD — параллелограмм, AC и BD — диагонали, пересекающиеся в точке O. Нужно доказать, что O — центр симметрии.
1. В параллелограмме диагонали делятся пополам, значит AO = OC и BO = OD.
2. AO = OC, следовательно, вершины A и C симметричны относительно точки O.
3. Углы BOF и EOD равны как вертикальные, углы FBO и ODE равны как накрест лежащие, а BO = OD. Значит, треугольники ABO и AEO равны, отсюда FO = OE.
4. Раз O является центром симметрии диагоналей и других элементов параллелограмма, то O — центр симметрии всей фигуры.
Вывод: O — центр симметрии параллелограмма ABCD.
Дано: ABCD — параллелограмм, диагонали AC и BD пересекаются в точке O. Необходимо доказать, что точка O является центром симметрии параллелограмма.
Рассмотрим свойства параллелограмма. Одним из основных свойств является то, что его диагонали делят друг друга пополам. Это означает, что точка пересечения диагоналей, точка O, делит каждую диагональ на две равные части. Следовательно, AO = OC и BO = OD.
Теперь докажем, что точка O является центром симметрии фигуры. Для этого нужно показать, что для любой точки параллелограмма существует симметричная ей точка, и их середина совпадает с точкой O.
1. Рассмотрим диагональ AC. Поскольку AO = OC, вершины A и C симметричны относительно точки O. Это означает, что точка O является серединой отрезка AC.
2. Аналогично рассмотрим диагональ BD. Поскольку BO = OD, вершины B и D также симметричны относительно точки O. Это означает, что точка O является серединой отрезка BD.
3. Теперь проверим симметрию для произвольной точки параллелограмма. Пусть P — произвольная точка внутри параллелограмма. Через точку P проведем прямые, параллельные сторонам AB и AD, которые пересекут стороны параллелограмма в точках Q, R, S, T. По свойству параллелограмма противоположные стороны равны и параллельны, а диагонали делят его на равные треугольники. Это гарантирует, что точка P имеет симметричную точку P’, которая расположена так, что отрезок PP’ проходит через точку O, а точка O является серединой этого отрезка.
4. Таким образом, для любой точки фигуры существует симметричная ей точка, и их середина совпадает с точкой O.
Вывод: точка O является центром симметрии параллелограмма, так как она делит пополам как диагонали, так и все отрезки, соединяющие симметричные точки фигуры.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.