
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 440 Атанасян — Подробные Ответы
На двух сторонах треугольника вне его построены квадраты. Докажите, что отрезок, соединяющий концы сторон квадратов, выходящих из одной вершины треугольника, в два раза больше медианы треугольника, выходящей из той же вершины.
Дано: ABCD — параллелограмм, BCDE и BNMA — квадраты, BO — медиана треугольника ABC. Требуется доказать, что NE = 2BO.
Решение: Построим точку O так, чтобы OD = OB и AO = OC. Поскольку BO — медиана, то ABCD является параллелограммом. Углы BOC и AOD равны как вертикальные, а также BO = OD и AO = OC, поэтому треугольники AOD и BOC равны. Из этого следует, что BC = AD. В квадрате BCDE сторона EB равна BC, а в квадрате BNMA сторона NB равна BA. Четырехугольники AEBN и ABAD равны, из чего следует, что EN = BD. Так как BD = 2BO, то NE = 2BO. Доказательство завершено.
Дано: ABCD — параллелограмм, BCDE и BNMA — квадраты, BO — медиана треугольника ABC. Требуется доказать, что NE = 2BO.
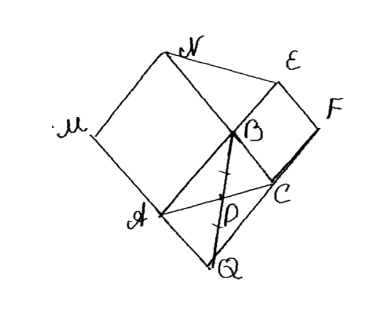
Решение:
Сначала построим точку O так, чтобы OD = OB и AO = OC. Это возможно, так как BO является медианой треугольника ABC, а медиана делит противоположную сторону пополам. В результате построения получаем, что ABCD — параллелограмм, поскольку его диагонали пересекаются и делятся пополам.
Углы BOC и AOD равны, так как они являются вертикальными. По построению отрезки BO и OD равны, а также AO и OC равны. Следовательно, треугольники AOD и BOC равны по двум сторонам и углу между ними. Из равенства треугольников следует, что BC = AD, так как эти стороны являются соответствующими в равных треугольниках.
Далее рассмотрим квадраты BCDE и BNMA. У квадрата BCDE сторона EB равна стороне BC, а у квадрата BNMA сторона NB равна стороне BA. Также углы при вершинах B и A равны 90 градусам, так как это свойства квадратов. На основании этого можно утверждать, что четырехугольники AEBN и ABAD равны по двум сторонам и углу между ними.
Из равенства этих четырехугольников следует, что EN = BD, так как эти отрезки являются соответствующими элементами равных фигур.
Теперь рассмотрим отрезок BD. В параллелограмме ABCD диагональ BD равна удвоенной медиане BO, то есть BD = 2BO. Так как EN = BD, то из этого следует, что NE = 2BO.
Доказательство завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!