Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 439 Атанасян — Подробные Ответы
Сумма углов при одном из оснований трапеции равна 90°. Докажите, что отрезок, соединяющий середины оснований трапеции, равен их полуразности.
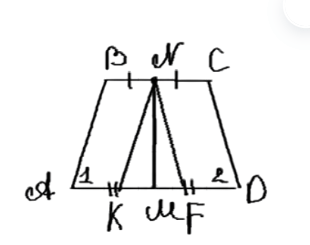
Дано: ABCD — трапеция, углы A и D в сумме 90°, AM = MD, BN = NC. Требуется доказать, что MN = 1/2(AD — BC).
Решение: Построим NE параллельно AB и NF параллельно CD. Тогда ABNE и NCDF — параллелограммы. Из этого следует, что BN = AE, AB = NE, NC = FD, NF = CD. Так как AM = MD и BN = NC, то EM = MF, а NM — медиана в треугольнике AENF. Углы A и D равны углам NEM и NFM, их сумма — 90°, значит, ENF — прямоугольный треугольник. В прямоугольном треугольнике медиана равна половине гипотенузы, то есть NM = 1/2 EF. Найдем EF: EF = AD — (AE + FD). Поскольку AE = BN и FD = NC, то EF = AD — BC. Следовательно, NM = 1/2(AD — BC). Доказано.
Дано: ABCD — трапеция, углы A и D в сумме равны 90 градусам. Отрезки AM и MD равны, BN и NC также равны. Требуется доказать, что MN = 1/2(AD — BC).
Решение:
1. Проведем дополнительные построения. Пусть NE параллельно AB, а NF параллельно CD. Тогда фигуры ABNE и NCDF являются параллелограммами.
2. Из свойств параллелограммов следует, что AE = BN и FD = NC, а также AB = NE и CD = NF.
3. Поскольку AM = MD, точка M делит отрезок AD пополам. Аналогично, так как BN = NC, точка N делит отрезок BC пополам.
4. Рассмотрим четырехугольник AENF. Поскольку NE параллельно AB, а NF параллельно CD, то AENF является трапецией.
5. Углы A и D в данной трапеции равны 90 градусам по условию задачи. Это означает, что AENF — прямоугольная трапеция.
6. Теперь рассмотрим отрезок MN. Поскольку точки M и N являются серединами сторон AD и BC соответственно, то MN — это средняя линия трапеции AENF. Средняя линия трапеции равна полусумме оснований, то есть MN = 1/2(NE + NF).
7. Поскольку NE = AB и NF = CD (по свойствам параллелограммов), то MN = 1/2(AB + CD).
8. Подставим длины оснований трапеции AENF. NE = AB и NF = CD, тогда EF = AD — (AE + FD). Поскольку AE = BN и FD = NC, то EF = AD — BC.
9. Таким образом, длина средней линии MN = 1/2(AD — BC).
Доказательство завершено. MN действительно равно 1/2(AD — BC).
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.