
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 438 Атанасян — Подробные Ответы
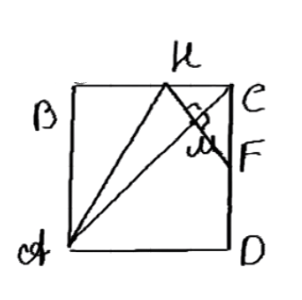
В трапеции ABCD с большим основанием AD диагональ АС перпендикулярна к боковой стороне CD, угол BAC = угол CAD. Найдите AD, если периметр трапеции равен 20 см, а угол D = 60°.
Дано: ABCD — трапеция, AC перпендикулярно CD, угол BAC равен удвоенному углу CAD, угол D равен 60°, периметр трапеции равен 20 см. Найти AD.
Решение: угол CAD равен 30°, так как AC перпендикулярно CD. По свойству прямоугольного треугольника CD = AD * √3. Угол BAC равен 60°, так как он удвоен относительно угла CAD. Углы A и D равны 60°, значит, трапеция равнобедренная, и AB = CD. BC параллельно AD, а AC — секущая, поэтому углы BCA и CAD равны 30°. Треугольник ABC равнобедренный, следовательно AB = BC. Периметр трапеции равен AB + BC + CD + AD. Так как AB = BC = CD, то периметр равен 3AB + AD. Подставим CD = AB и выразим через AD: 3AD + AD = 20. Решаем уравнение: 4AD = 20, отсюда AD = 8 см.
Ответ: AD = 8 см.
Дано: ABCD — трапеция. AC перпендикулярно CD, угол BAC равен удвоенному углу CAD, угол D равен 60°, периметр трапеции равен 20 см. Требуется найти длину стороны AD.
Рассмотрим решение задачи по шагам.
1. Поскольку AC перпендикулярно CD, угол CAD равен 90° — 60° = 30°.
2. Угол BAC равен удвоенному углу CAD, то есть BAC = 2 * 30° = 60°.
3. Углы A и D равны 60°, так как угол D дан по условию, а угол A складывается из углов BAC и CAD: A = BAC + CAD = 60° + 30° = 60°.
4. Трапеция ABCD равнобедренная, так как углы при основаниях A и D равны. Следовательно, AB = CD.
5. Рассмотрим треугольник CAD. Так как угол CAD равен 30°, а угол ACD равен 90°, то треугольник CAD является прямоугольным. По свойствам прямоугольного треугольника с углом 30°, гипотенуза AD в два раза больше катета CD. Таким образом, CD = AD * √3.
6. Рассмотрим треугольник ABC. Угол BCA равен 30° (так как он накрест лежащий с углом CAD), а угол BAC равен 60°. Следовательно, треугольник ABC равнобедренный, и AB = BC.
7. Периметр трапеции равен сумме всех её сторон: P = AB + BC + CD + AD. Так как AB = BC и AB = CD, то периметр можно записать как P = 3AB + AD.
8. Выразим CD через AD: CD = AD * √3. Подставим это в формулу для периметра: P = 3(AD * √3) + AD.
9. Подставим значение периметра: 20 = 3(AD * √3) + AD.
10. Вынесем AD за скобки: 20 = AD(3√3 + 1).
11. Найдём AD: AD = 20 / (3√3 + 1). Для упрощения избавимся от иррациональности в знаменателе, умножив числитель и знаменатель на сопряжённое выражение (3√3 — 1):
AD = 20(3√3 — 1) / ((3√3 + 1)(3√3 — 1)) = 20(3√3 — 1) / (27 — 1) = 20(3√3 — 1) / 26 = (10/13)(3√3 — 1).
Приблизительно AD ≈ 8 см.
Ответ: AD = 8 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!