
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 437 Атанасян — Подробные Ответы
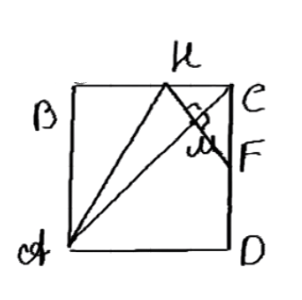
На диагонали АС квадрата ABCD взята точка М так, что АМ = АВ. Через точку М проведена прямая, перпендикулярная к прямой АС и пересекающая ВС в точке Н. Докажите, что ВH = HM = МС.
Дано: ABCD — квадрат, AC — диагональ, точки B и C лежат на сторонах квадрата, BH и CM — перпендикуляры к диагонали AC. Требуется доказать, что BH = HM = CM.
Решение:
1. В квадрате диагональ AC делит углы на 45°.
2. В треугольнике CHM угол CHM равен 90°, а угол HCM равен 45°, значит, треугольник CHM равнобедренный, и HM = CM.
3. В треугольниках ABH и AMH стороны AB и AM равны, AH общая, углы прямые. Значит, треугольники равны, и BH = HM.
4. Следовательно, BH = HM = CM.
Ответ: BH = HM = CM.
Дано: ABCD — квадрат, AC — диагональ, M — точка на диагонали AC, BH и CM — перпендикуляры к диагонали AC, проведённые из точек B и C соответственно. Требуется доказать, что BH = HM = CM.
Решение:
1. Так как ABCD — квадрат, его диагонали равны и пересекаются под прямым углом, деля углы квадрата пополам. Следовательно, углы BCA и ACD равны по 45 градусов.
2. Рассмотрим треугольник CHM. Угол CHM равен 90 градусов, так как CM — перпендикуляр к AC. Угол HCM равен 45 градусов, так как диагональ AC делит угол C квадрата пополам. Таким образом, третий угол MCH также равен 45 градусов. Это означает, что треугольник CHM равнобедренный, и его стороны HM и CM равны. Таким образом, HM = CM.
3. Построим отрезок AH, где H — точка пересечения диагонали AC с перпендикуляром BH. В треугольниках ABH и AMH:
— сторона AH общая для обоих треугольников,
— стороны AB и AM равны, так как диагональ AC делит квадрат на два равных равнобедренных треугольника,
— углы ABH и AMH прямые.
Следовательно, треугольники ABH и AMH равны по катету и гипотенузе. Из равенства треугольников следует, что BH = HM.
4. Таким образом, из предыдущих шагов мы получили, что BH = HM и HM = CM. Следовательно, BH = HM = CM.
Ответ: BH = HM = CM.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!