ГДЗ по Геометрии 8 класс Номер 436 Атанасян — Подробные Ответы

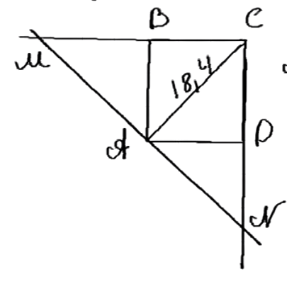
 Диагональ АС квадрата ABCD равна 18,4 см. Прямая, проходящая через точку А и перпендикулярная к прямой АС, пересекает прямые ВС и CD соответственно в точках М и N. Найдите MN. 

Дано: ABCD — квадрат, AC — диагональ, AC = 18,4 см. Углы ∠BCA и ∠ACD равны 45°.

В треугольнике CAM угол ∠CAM = 90°, ∠CMA = 45°, значит треугольник равнобедренный, и AM = AC = 18,4 см. Аналогично, в треугольнике CAN угол ∠CAN = 90°, ∠CNA = 45°, треугольник равнобедренный, и AN = AC = 18,4 см. Длина MN равна MA + AN = 18,4 + 18,4 = 36,8 см. Ответ: 36,8 см.

Дано: ABCD — квадрат, AC — диагональ, AC = 18,4 см. Точка M лежит на стороне BC, а точка N лежит на стороне CD. Требуется найти длину отрезка MN.

Решение:

Поскольку ABCD — квадрат, диагональ AC делит угол C пополам. Это означает, что углы ∠BCA и ∠ACD равны по 45 градусов.

Рассмотрим треугольник CAM. Угол ∠CAM равен 90 градусам, так как AC — диагональ квадрата, а угол ∠CMA равен 45 градусам, так как диагональ AC делит угол квадрата пополам. Таким образом, треугольник CAM является равнобедренным, и стороны AM и AC равны. Следовательно, AM = AC = 18,4 см.

Аналогично рассмотрим треугольник CAN. Угол ∠CAN равен 90 градусам, а угол ∠CNA равен 45 градусам по той же причине, что и в предыдущем случае. Это означает, что треугольник CAN также является равнобедренным, и стороны AN и AC равны. Следовательно, AN = AC = 18,4 см.

Теперь найдем длину отрезка MN. Поскольку точки M и N лежат на сторонах BC и CD квадрата соответственно, а отрезок MN параллелен диагонали AC, длина MN равна сумме длин MA и AN. Таким образом, MN = MA + AN = 18,4 + 18,4 = 36,8 см.

Ответ: 36,8 см.