
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 435 Атанасян — Подробные Ответы
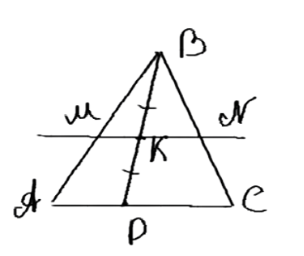
Докажите, что середина отрезка, соединяющего вершину треугольника с любой точкой противоположной стороны, лежит на отрезке с концами в серединах двух других сторон.
Дано: ΔABC, AC и BD пересекаются. K — середина BD.
Решение: Проведем через точку K прямую, параллельную AC. Пусть она пересекает AB в точке M, а BC в точке N. Так как K — середина BD, а MN параллельна AC, то по теореме Фалеса M делит AB пополам, а N делит BC пополам. Следовательно, AM = MB и BN = NC.
Дано: ΔABC, AC и BD пересекаются. Точка K является серединой отрезка BD. Необходимо доказать, что AM = MB и BN = NC.
Решение:
1. Пусть точка K — середина отрезка BD. Через точку K проведем прямую, параллельную AC. Обозначим точки пересечения этой прямой с отрезками AB и BC как M и N соответственно. Таким образом, MN параллельна AC.
2. Рассмотрим отрезок AB. Так как MN параллельна AC, а точка K является серединой BD, то по теореме Фалеса прямая MN делит отрезок AB на две равные части. Следовательно, точка M является серединой отрезка AB, то есть AM = MB.
3. Аналогично рассмотрим отрезок BC. Так как MN параллельна AC, а точка K является серединой BD, то по теореме Фалеса прямая MN делит отрезок BC на две равные части. Следовательно, точка N является серединой отрезка BC, то есть BN = NC.
Вывод: доказано, что AM = MB и BN = NC.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!