
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 434 Атанасян — Подробные Ответы
Докажите, что точка пересечения диагоналей ромба равноудалена от его сторон.
Дано: ABCD — ромб, диагонали AC и BD пересекаются под прямым углом в точке O. Проведены перпендикуляры BM, BN, OF, OE к сторонам ромба. Требуется доказать, что ON = OM = OE = OF.
Решение:
1) В ромбе диагонали делят углы пополам и пересекаются под прямым углом. Углы ∠ABO и ∠OBC равны, ∠ADO и ∠ODC равны, ∠BAO = ∠DAO, ∠BCO = ∠OCD.
2) Треугольники BNO и BMO равны, так как имеют общую сторону BO, равные углы ∠NBO и ∠BMO (BD — биссектриса ∠ABC) и прямые углы ∠ONB и ∠OMB. Следовательно, ON = OM.
3) Треугольники FOD и EOD равны, так как имеют общую сторону OD, равные углы ∠FDO и ∠ODE (BD — биссектриса ∠ADC) и прямые углы ∠OFD и ∠OED. Следовательно, FO = OE.
4) Диагонали ромба делят друг друга пополам, поэтому AO = OC. Треугольники AON и COE равны, так как AO = CO, углы ∠OAN и ∠OCE равны (AC — биссектриса ∠BAD и ∠BCD), а углы ∠ONA и ∠OEC прямые. Следовательно, NO = OE.
5) Аналогично из равенства треугольников BMO и FOD следует, что OM = FO.
Вывод: ON = OM = OE = OF. Доказательство завершено.
Дано: ABCD — ромб. Его диагонали AC и BD пересекаются в точке O под прямым углом. Проведены перпендикуляры BM, BN, OF, OE к сторонам ромба. Требуется доказать, что отрезки ON, OM, OE и OF равны.
Решение:
1. В ромбе диагонали AC и BD пересекаются под прямым углом в точке O и делят углы ромба пополам. Это означает, что углы ∠ABO и ∠OBC равны, углы ∠ADO и ∠ODC равны, а также ∠BAO = ∠DAO и ∠BCO = ∠OCD. Таким образом, диагонали являются биссектрисами углов ромба.
2. Рассмотрим треугольники BNO и BMO. У них общая сторона BO, углы ∠NBO и ∠BMO равны, так как диагональ BD делит угол ∠ABC пополам. Кроме того, углы ∠ONB и ∠OMB прямые по условию, так как BN и BM являются перпендикулярами к сторонам ромба. Следовательно, треугольники BNO и BMO равны по гипотенузе и острому углу. Из равенства треугольников следует, что ON = OM.
3. Аналогично рассмотрим треугольники FOD и EOD. У них общая сторона OD, углы ∠FDO и ∠ODE равны, так как диагональ BD делит угол ∠ADC пополам. Углы ∠OFD и ∠OED прямые по условию, так как OF и OE являются перпендикулярами к сторонам ромба. Следовательно, треугольники FOD и EOD равны по гипотенузе и острому углу. Из равенства треугольников следует, что FO = OE.
4. В ромбе диагонали AC и BD делят друг друга пополам. Это означает, что AO = OC и BO = OD. Рассмотрим треугольники AON и COE. У них AO = CO, углы ∠OAN и ∠OCE равны, так как диагональ AC делит углы ∠BAD и ∠BCD пополам, а углы ∠ONA и ∠OEC прямые, так как ON и OE перпендикулярны сторонам ромба. Следовательно, треугольники AON и COE равны по гипотенузе и острому углу. Из равенства треугольников следует, что NO = OE.
5. Аналогично из равенства треугольников BMO и FOD можно показать, что OM = FO.
6. Таким образом, доказано, что ON = OM = OE = OF. Все отрезки равны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


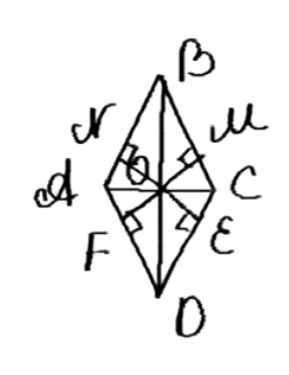

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!