
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 433 Атанасян — Подробные Ответы
Из вершины В ромба ABCD проведены перпендикуляры ВК и ВМ к прямым AD и DC. Докажите, что луч BD является биссектрисой угла КВМ.
Дано: ABCD — ромб. Из вершины B проведены перпендикуляры BK и BM к сторонам AD и DC. Требуется доказать, что BD — биссектриса угла KBM.
Решение: Поскольку ABCD — ромб, его диагонали пересекаются под прямым углом и являются биссектрисами углов. Рассмотрим треугольники BMC и BKA. У них равны стороны AB и BC, углы BMC и BKA прямые, а диагональ BD — общая сторона. По признаку равенства прямоугольных треугольников они равны, следовательно, углы CBM и ABK равны. Поскольку диагональ BD делит угол ABC пополам, то углы MBD и DBK равны. Это доказывает, что BD — биссектриса угла KBM.
Дано: ABCD — ромб. Из вершины B проведены перпендикуляры BK и BM к сторонам AD и DC соответственно. Требуется доказать, что диагональ BD является биссектрисой угла KBM.
Решение:
1. Поскольку ABCD является ромбом, его диагонали пересекаются под прямым углом. Кроме того, диагонали ромба являются биссектрисами противоположных углов. Следовательно, диагональ BD делит угол ABC на два равных угла.
2. Рассмотрим треугольники BMC и BKA. В ромбе стороны AB и BC равны, так как все стороны ромба равны по определению. Углы BMC и BKA являются прямыми по условию задачи, так как BM и BK являются перпендикулярами к сторонам DC и AD соответственно. Также диагональ BD является общей стороной для треугольников BMC и BKA.
3. По признаку равенства прямоугольных треугольников (гипотенуза и катет), треугольники BMC и BKA равны. Из равенства треугольников следует, что углы CBM и ABK равны, так как они являются соответствующими углами равных треугольников.
4. Поскольку диагональ BD делит угол ABC пополам, то углы MBD и DBK равны. Это означает, что диагональ BD является биссектрисой угла KBM.
Таким образом, доказано, что диагональ BD является биссектрисой угла KBM.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


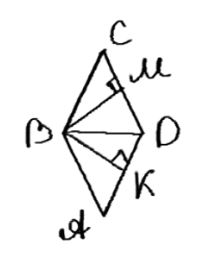

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!