Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 431 Атанасян — Подробные Ответы
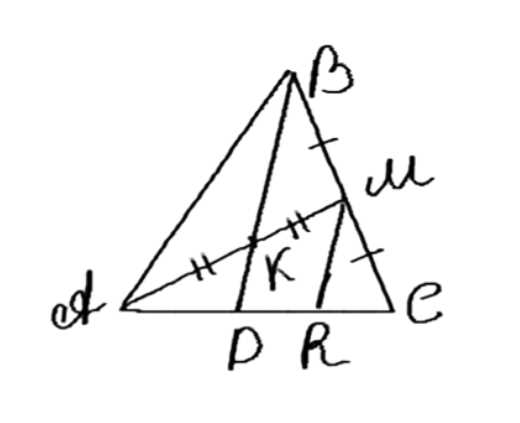
Точка К — середина медианы АМ треугольника АВС. Прямая ВК пересекает сторону АС в точке D. Докажите, что AD = 1/3 AC.
Дано: треугольник ABC, AM — медиана, K ∈ AM, AK = KM, BK ∩ AC = D. Доказать: AD = 1/3 AC.
Доказательство:
1) Проведем MF || BD, тогда DF = FC (по теореме Фалеса).
2) KD || MF, так как MF || BD.
3) По теореме Фалеса, AK = KM ⇒ AD = DF.
4) Из DF = FC и AD = DF ⇒ AD = DF = FC.
5) AC = AD + DF + FC = 3AD ⇒ AD = 1/3 AC.
Вывод: AD = 1/3 AC.
Дано: треугольник ABC, AM — медиана, K ∈ AM, AK = KM, BK ∩ AC = D. Доказать: AD = 1/3 AC.
Доказательство:
1) Поскольку AM — медиана, то BM = MC.
2) Точка K делит AM пополам, поэтому AK = KM.
3) Проведем прямую MF, параллельную BD, где F — точка на стороне AC.
4) По теореме Фалеса, так как MF || BD и BM = MC, то DF = FC.
5) Рассмотрим треугольник AMF. Прямая KD параллельна MF, так как MF || BD, а KD лежит на BD.
6) По теореме Фалеса, так как AK = KM и KD || MF, то AD = DF.
7) Из пункта 4 известно, что DF = FC. Следовательно, AD = DF = FC.
8) Длина стороны AC равна сумме AD, DF и FC: AC = AD + DF + FC.
9) Подставим AD = DF = FC в выражение: AC = AD + AD + AD = 3AD.
10) Отсюда AD = 1/3 AC.
Вывод: Доказано, что AD = 1/3 AC.
Это решение включает все необходимые шаги с подробными объяснениями, чтобы убедиться, что каждый этап доказательства понятен и логически обоснован.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.