
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 422 Атанасян — Подробные Ответы
Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?
Центр симметрии — точка, относительно которой фигура симметрична.
а) Отрезок имеет центр симметрии — его середину.
б) Луч не имеет центра симметрии, так как он бесконечен в одном направлении.
в) Пара пересекающихся прямых имеет центр симметрии — точку их пересечения.
г) Квадрат имеет центр симметрии — точку пересечения диагоналей.
Ответ: а) да; б) нет; в) да; г) да.
Центр симметрии — это точка, относительно которой фигура симметрична. Рассмотрим каждую фигуру:
а) Отрезок имеет центр симметрии. Это его середина. Если взять любую точку на отрезке, симметричная ей точка также будет лежать на отрезке.
б) Луч не имеет центра симметрии. Луч имеет начало, но бесконечно продолжается в одном направлении. Невозможно найти точку, относительно которой луч будет симметричен.
в) Пара пересекающихся прямых имеет центр симметрии. Это точка их пересечения. Каждая прямая симметрична относительно этой точки.
г) Квадрат имеет центр симметрии. Это точка пересечения диагоналей. Любая точка квадрата имеет симметричную точку относительно этого центра.
Ответ: а) да; б) нет; в) да; г) да.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


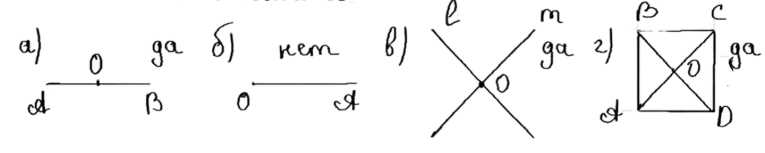

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!