
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 420 Атанасян — Подробные Ответы
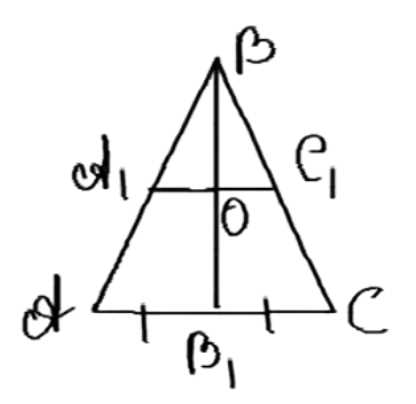
Докажите, что прямая, содержащая биссектрису равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника.
Дано: ΔABC — равнобедренный, ВН — биссектриса угла B.
Доказательство:
1. В равнобедренном треугольнике AB = BC.
2. Биссектриса ВН делит угол B на равные части.
3. ВН также является медианой и высотой, поэтому AH = HC.
4. Прямая ВН делит ΔABC на два равных прямоугольных треугольника: ΔABH и ΔCBH.
5. Каждая точка AB имеет симметричную точку на BC относительно ВН.
6. Следовательно, ВН — ось симметрии ΔABC.
Дано: ΔABC — равнобедренный треугольник, ВН — биссектриса угла B.
Доказать: ВН — ось симметрии.
Доказательство:
1. В равнобедренном треугольнике ΔABC стороны AB и BC равны по определению.
2. Биссектриса ВН делит угол B на два равных угла, так как она является биссектрисой.
3. По свойству равнобедренного треугольника, биссектриса, проведенная к основанию, также является медианой и высотой.
4. Следовательно, ВН делит основание AC на две равные части, то есть AH = HC.
5. Прямая ВН делит треугольник ΔABC на два равных прямоугольных треугольника: ΔABH и ΔCBH.
6. В этих треугольниках стороны AB и BC равны, углы при вершине B равны, и стороны AH и HC равны.
7. Каждая точка стороны AB имеет симметричную точку на стороне BC относительно прямой ВН.
8. Это означает, что если взять любую точку на AB, то её отражение относительно ВН будет лежать на BC.
9. Таким образом, прямая ВН является осью симметрии треугольника ΔABC.
10. Это подтверждает, что ВН не только биссектриса, но и ось симметрии, разделяющая треугольник на две равные части.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!