
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 416 Атанасян — Подробные Ответы
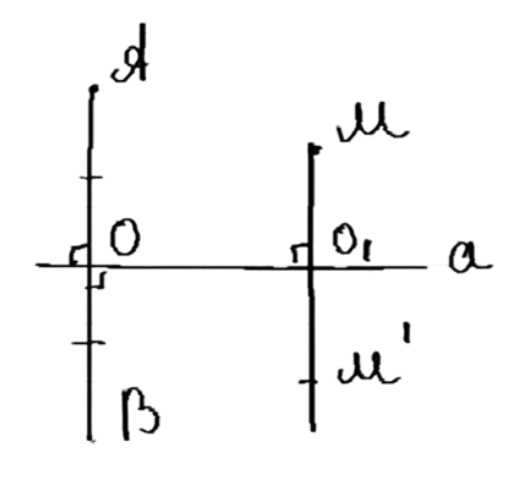
Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.
Решение задачи с детализацией:
1. Построение прямой а и точки С:
— Проведи прямую а с помощью линейки.
— Отметь точку С на прямой а.
2. Восстановление перпендикуляра к точке С:
— Построй окружность с центром в точке С и произвольным радиусом. Пересечение окружности с прямой а даст точки Е и F.
— Построй окружность с центром в точке F и радиусом FE.
— Построй окружность с центром в точке Е и радиусом FE.
— Пересечение этих окружностей даст точку D.
— Проведи прямую через точки D и С. Это будет перпендикуляр к прямой а в точке С.
— Отметь точку А на перпендикуляре.
— Построй окружность с центром в точке С и радиусом АС. Пересечение окружности с перпендикуляром даст точку В, симметричную точке А.
3. Восстановление перпендикуляра к точке К:
— Построй окружность с центром в точке К и произвольным радиусом. Пересечение окружности с прямой а даст точки М и Р.
— Построй окружность с центром в точке М и радиусом МР.
— Построй окружность с центром в точке Р и радиусом МР.
— Пересечение этих окружностей даст точку N.
— Проведи прямую через точки К и N. Это будет перпендикуляр к прямой а в точке К.
— Отметь точку М на перпендикуляре.
— Построй окружность с центром в точке К и радиусом МК. Пересечение окружности с перпендикуляром даст точку М’, симметричную точке М.
4. Построение окружности с центром О и радиусом ОМ:
— Проведи прямую через точку М и точку О.
— Построй окружность с центром в точке О и радиусом ОМ.
— Пересечение окружности с перпендикуляром через точку М даст точку М’, которая является искомой.
Это полное решение с детализацией каждого шага. Все построения выполняются с использованием циркуля и линейки для точности.
Решение 1:
1. Построй прямую а и отметь точку С.
2. Восстанови перпендикуляр к точке С:
— Построй окружность с центром С и произвольным радиусом, получи точки Е и F на а.
— Построй окружности с центрами в точках F и E и радиусом FE, отметь точку D на их пересечении.
— Проведи через D и С перпендикулярную прямую, отметь на ней точку А.
— Построй окружность с центром С и радиусом АС, отметь симметричную точке А точку В.
3. Восстанови перпендикуляр к точке К:
— Построй окружность с центром К и произвольным радиусом, получи точки М и Р на а.
— Построй окружности с центрами в точках М и Р и радиусом МР, отметь точку N на их пересечении.
— Проведи через К и N перпендикулярную прямую, отметь на ней точку М.
— Построй окружность с центром К и радиусом МК, отметь симметричную точке М точку М’.
Решение 2:
1. Проведи к прямой а перпендикуляр через точку М.
2. Построй окружность с центром О и радиусом ОМ.
3. При пересечении окружности с перпендикуляром получи точку М’ — искомую.
Оба решения используют построение окружностей и перпендикуляров для достижения результата.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!