
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 414 Атанасян — Подробные Ответы
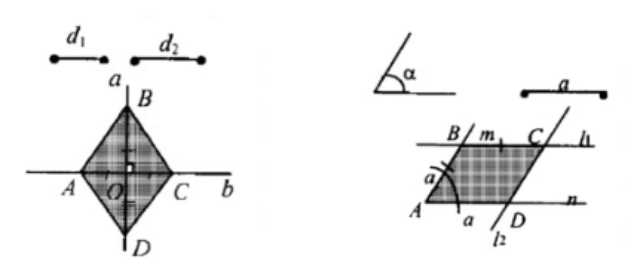
Постройте ромб: а) по двум диагоналям; б) по стороне и углу.
а) Построение ромба по двум диагоналям:
1. Проводим две перпендикулярные прямые, пересекающиеся в точке O.
2. Откладываем отрезки OA, OB, OC и OD, равные половине длины диагоналей.
3. Соединяем точки A, B, C и D прямыми.
4. Получаем ромб ABCD.
б) Построение ромба по стороне и углу:
1. Проводим угол A, равный заданному углу.
2. Откладываем отрезок AB, равный длине стороны a.
3. Через точку B проводим прямую l1, параллельную одной стороне угла.
4. Откладываем отрезок BC, равный длине стороны a.
5. Через точку C проводим прямую l2, параллельную другой стороне угла.
6. Точка пересечения прямых l1 и l2 будет точкой D.
7. Получаем ромб ABCD.
а) Построение ромба по двум диагоналям:
1. Проводим две перпендикулярные прямые, которые пересекаются в точке O. Это будут оси диагоналей ромба.
2. От точки O откладываем отрезки OA и OB, равные половине длины первой диагонали.
3. От точки O откладываем отрезки OC и OD, равные половине длины второй диагонали.
4. Соединяем точки A, B, C и D прямыми линиями.
5. Получаем ромб ABCD, где диагонали пересекаются под прямым углом и делятся пополам.
б) Построение ромба по стороне и углу:
1. Проводим угол A, равный заданному углу. Это будет один из углов ромба.
2. От вершины угла A откладываем отрезок AB, равный длине стороны ромба.
3. Через точку B проводим прямую l1, параллельную одной из сторон угла A.
4. От точки B откладываем отрезок BC, равный длине стороны ромба.
5. Через точку C проводим прямую l2, параллельную другой стороне угла A.
6. Точка пересечения прямых l1 и l2 будет точкой D.
7. Соединяем точки A, B, C и D прямыми линиями.
8. Получаем ромб ABCD, где все стороны равны, а углы соответствуют заданным условиям.
Каждый шаг выполняется с использованием циркуля и линейки, соблюдая точность измерений и построений.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!