
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 412 Атанасян — Подробные Ответы
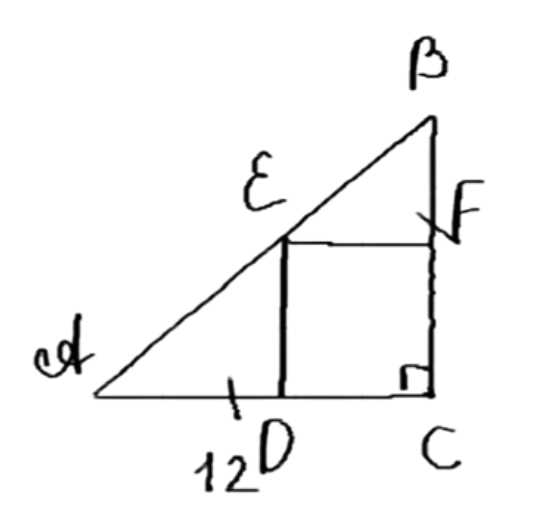
Даны равнобедренный прямоугольный треугольник ABC с прямым углом С, катетом АС = 12 см и квадрат CDEF, такой, что две его стороны лежат на катетах, а вершина Е — на гипотенузе треугольника. Найдите периметр квадрата.
Дано: треугольник ABC — прямоугольный и равнобедренный, угол C = 90°, AC = 12 см, CDEF — квадрат, E ∈ AB.
Решение:
1. Треугольник ABC — равнобедренный, значит, AC = CB = 12 см, углы A и B равны 45°.
2. CDEF — квадрат, поэтому CD = DE = EF = CF.
3. Треугольник ADE — равнобедренный, так как угол A = 45°, значит, AD = DE.
4. Треугольник EFB — равнобедренный, так как угол B = 45°, значит, CF = FB.
5. AC = AD + DC = 2DC = 12 см, откуда DC = 6 см.
6. CB = CF + FB = 2CF = 12 см, откуда CF = 6 см.
7. Периметр квадрата CDEF равен 4 · DC = 4 · 6 = 24 см.
Ответ: 24 см.
Дано: треугольник ABC — прямоугольный и равнобедренный, угол C = 90°, AC = 12 см, CDEF — квадрат, E ∈ AB.
Найти: периметр квадрата CDEF.
Решение:
1. Треугольник ABC — прямоугольный и равнобедренный, значит, его катеты равны: AC = CB = 12 см. Углы при основании равны 45°, то есть угол A = угол B = 45°.
2. CDEF — квадрат, поэтому все его стороны равны: CD = DE = EF = CF.
3. Рассмотрим треугольник ADE. Угол A = 45°, а угол ADE = 90° (так как CDEF — квадрат). Следовательно, угол AED = 45°, и треугольник ADE — равнобедренный. Отсюда AD = DE.
4. Рассмотрим треугольник EFB. Угол B = 45°, а угол EFB = 90° (так как CDEF — квадрат). Следовательно, угол FEB = 45°, и треугольник EFB — равнобедренный. Отсюда CF = FB.
5. Выразим AC через стороны квадрата: AC = AD + DC. Поскольку AD = DE, а DE = DC (так как CDEF — квадрат), то AC = DC + DC = 2DC. Подставляем значение AC: 2DC = 12 см, откуда DC = 6 см.
6. Аналогично выразим CB через стороны квадрата: CB = CF + FB. Поскольку CF = FB, то CB = CF + CF = 2CF. Подставляем значение CB: 2CF = 12 см, откуда CF = 6 см.
7. Периметр квадрата CDEF равен сумме всех его сторон: P = CD + DE + EF + CF. Поскольку все стороны равны 6 см, то P = 6 + 6 + 6 + 6 = 24 см.
Ответ: периметр квадрата CDEF равен 24 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!