ГДЗ по Геометрии 8 класс Номер 410 Атанасян — Подробные Ответы

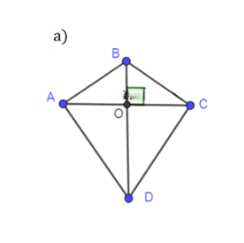
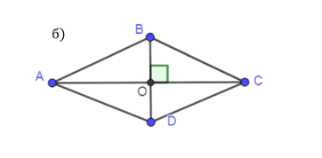
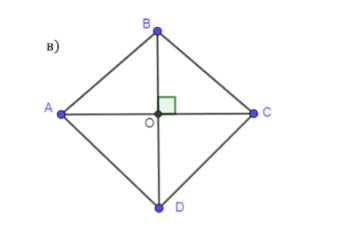
Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?

Дано: ABCD — четырёхугольник, диагонали AC и BD пересекаются в точке O. Известно: AO = OC, BO = OD, BD = AC.

Доказательство:
1) Поскольку AO = OC и BO = OD, ABCD — параллелограмм.
2) В параллелограмме диагонали делятся пополам, но не обязательно равны.
3) По условию BD = AC, что делает ABCD прямоугольником.
4) Прямоугольник с равными диагоналями, которые делятся пополам, является квадратом.
Ответ: ABCD — квадрат.

Дано: ABCD — четырёхугольник, диагонали AC и BD пересекаются в точке O.
Известно:
1) AO = OC (диагонали делятся пополам),
2) BO = OD (диагонали делятся пополам),
3) BD = AC (диагонали равны по длине).

Доказательство:
1) Поскольку AO = OC и BO = OD, четырёхугольник ABCD является параллелограммом. Это следует из признака параллелограмма: если диагонали четырёхугольника делятся пополам, то он является параллелограммом.
2) В параллелограмме противоположные стороны равны и параллельны, а противоположные углы равны.
3) По условию BD = AC, что является дополнительным свойством. В параллелограмме диагонали не обязательно равны по длине, но если они равны, то это прямоугольник.
4) Прямоугольник — это параллелограмм, у которого все углы прямые (90 градусов).
5) Если в прямоугольнике диагонали делятся пополам и равны по длине, то это квадрат.
6) Таким образом, ABCD — квадрат, так как он удовлетворяет всем свойствам квадрата: все стороны равны, все углы прямые, диагонали равны и делятся пополам.

Ответ: ABCD — квадрат.

Дополнительные детали:
— Квадрат — это частный случай ромба и прямоугольника, сочетающий их свойства.
— В квадрате диагонали не только равны, но и перпендикулярны друг другу, а также делят углы пополам.
— Данное решение подтверждает, что ABCD обладает всеми необходимыми свойствами квадрата.