
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 405 Атанасян — Подробные Ответы
В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами.
Дано: ABCD — ромб, AB = BD.
Найти: ∠A, ∠B, ∠C, ∠D; ∠ABD, ∠BAC.
Решение:
1) ABCD — ромб, все стороны равны: AB = BC = CD = AD.
2) AB = BD, значит, BD = AB = AD, треугольник ABD — равносторонний, ∠A = 60°.
3) Треугольник BDC также равносторонний, ∠C = 60°.
4) Угол B = ∠ABD + ∠DBC = 60° + 60° = 120°.
5) Угол D = ∠ADB + ∠BDC = 60° + 60° = 120°.
6) Диагонали ромба — биссектрисы, ∠ABD = ∠B / 2 = 120° / 2 = 60°, ∠BAC = ∠A / 2 = 60° / 2 = 30°.
Ответ: ∠A = 60°, ∠B = 120°, ∠C = 60°, ∠D = 120°; ∠ABD = 60°, ∠BAC = 30°.
Дано: ABCD — ромб, AB = BD.
Найти:
а) ∠A, ∠B, ∠C, ∠D;
б) ∠ABD, ∠BAC.
Решение:
а)
1) ABCD — ромб, следовательно, все его стороны равны: AB = BC = CD = AD.
2) По условию AB = BD, значит, BD также равно сторонам ромба.
3) Рассмотрим треугольник ABD. В нем AB = BD = AD, следовательно, треугольник ABD — равносторонний. В равностороннем треугольнике все углы равны 60°, поэтому ∠A = ∠ABD = ∠ADB = 60°.
4) Рассмотрим треугольник BDC. В нем BD = BC = CD, следовательно, треугольник BDC также равносторонний. Поэтому ∠C = ∠CBD = ∠CDB = 60°.
5) Угол B ромба состоит из двух углов: ∠ABD и ∠DBC. Поскольку каждый из них равен 60°, то ∠B = 60° + 60° = 120°.
6) Аналогично, угол D ромба состоит из углов ∠ADB и ∠BDC, каждый из которых равен 60°, поэтому ∠D = 60° + 60° = 120°.
б)
1) В ромбе диагонали являются биссектрисами углов. Это означает, что диагональ BD делит угол B на два равных угла: ∠ABD и ∠DBC. Поскольку ∠B = 120°, то ∠ABD = 120° / 2 = 60°.
2) Диагональ AC делит угол A на два равных угла: ∠BAC и ∠CAD. Поскольку ∠A = 60°, то ∠BAC = 60° / 2 = 30°.
Ответ:
а) ∠A = 60°, ∠B = 120°, ∠C = 60°, ∠D = 120°;
б) ∠ABD = 60°, ∠BAC = 30°.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


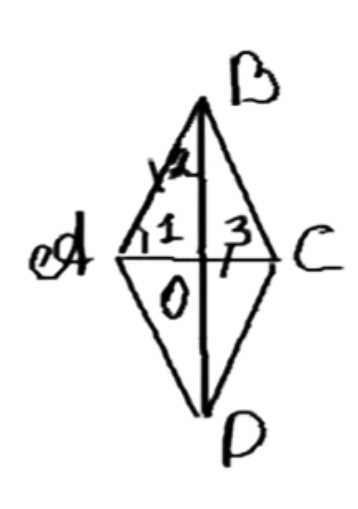

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!