ГДЗ по Геометрии 8 класс Номер 404 Атанасян — Подробные Ответы

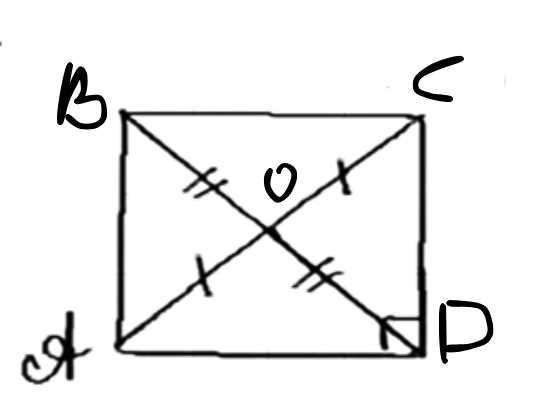
Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.

Дано: ΔABC — прямоугольный треугольник, OC — медиана. Доказать: OC = 1/2 AB.

Доказательство:
1) Продлим медиану OC до точки D так, чтобы OD = OC. Соединим точки A, B, C, D, получив четырехугольник ABCD.
2) Поскольку диагонали AC и BD делятся точкой O пополам, ABCD — параллелограмм.
3) Угол C равен 90°, поэтому ABCD — прямоугольник.
4) В прямоугольнике диагонали равны и делятся пополам, значит, BO = OD = OC = AO.
5) AB = AO + OB = OC + OC = 2OC.
6) Отсюда OC = 1/2 AB.

Доказано.

Дано: ΔABC — прямоугольный треугольник, OC — медиана.
Доказать: OC = 1/2 AB.

Доказательство:
1) Продлим медиану OC за точку O и отметим на продолжении точку D так, чтобы OD = OC. Соединим точки A, B, C, D, получив четырехугольник ABCD.
2) Поскольку диагонали AC и BD четырехугольника ABCD делятся точкой O пополам (AO = OC и BO = OD), ABCD является параллелограммом по признаку параллелограмма.
3) В ΔABC угол C равен 90°, поэтому все углы параллелограмма ABCD также равны 90°. Следовательно, ABCD — прямоугольник.
4) В прямоугольнике диагонали равны и делятся пополам, поэтому AC = BD и BO = OD = OC = AO.
5) Рассмотрим отрезок AB. В прямоугольнике AB = CD, а также AB = AO + OB. Поскольку AO = OC и OB = OD, то AB = OC + OC = 2OC.
6) Из равенства AB = 2OC следует, что OC = 1/2 AB.

Таким образом, доказано, что медиана OC прямоугольного треугольника ΔABC равна половине гипотенузы AB.