
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 403 Атанасян — Подробные Ответы
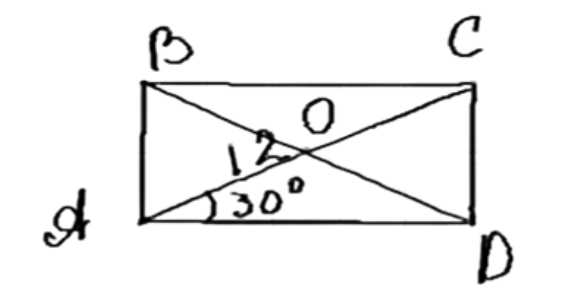
В прямоугольнике ABCD диагонали пересекаются в точке О.
Найдите периметр треугольника AOB, если ∠CAD = 30°, АС = 12 см.
Дано: ABCD — прямоугольник, BD и AC — диагонали, пересекающиеся в точке O, ∠CAD = 30°, AC = 12 см. Найти периметр треугольника AOB.
Решение:
1) В прямоугольнике диагонали равны и делятся пополам, поэтому AO = OC = 6 см.
2) В прямоугольном треугольнике ACD с углом 30° катет CD равен половине гипотенузы AC, то есть CD = 6 см.
3) По свойству прямоугольника AB = CD = 6 см.
4) Диагонали делятся пополам, значит, BO = OD = 6 см.
5) Периметр треугольника AOB равен AO + OB + AB = 6 + 6 + 6 = 18 см.
Ответ: 18 см.
Дано: ABCD — прямоугольник, BD и AC — диагонали, пересекающиеся в точке O, ∠CAD = 30°, AC = 12 см.
Найти: периметр треугольника AOB (PAOB).
Решение:
1) В прямоугольнике диагонали равны и делятся точкой пересечения пополам. Следовательно, AO = OC = AC / 2 = 12 / 2 = 6 см.
2) Рассмотрим прямоугольный треугольник ACD, где ∠CAD = 30°. В таком треугольнике катет, лежащий напротив угла 30°, равен половине гипотенузы. Таким образом, CD = AC / 2 = 12 / 2 = 6 см.
3) По свойству прямоугольника противоположные стороны равны, поэтому AB = CD = 6 см.
4) Диагонали прямоугольника делятся точкой O пополам, значит, BO = OD = AO = 6 см.
5) Периметр треугольника AOB равен сумме длин его сторон: PAOB = AO + OB + AB = 6 + 6 + 6 = 18 см.
Ответ: 18 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!