ГДЗ по Геометрии 8 класс Номер 396 Атанасян — Подробные Ответы

Разделите данный отрезок AB на п равных частей.
Решение
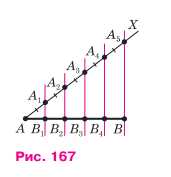
Проведём луч АХ, не лежащий на прямой АВ, и на нём от точки А отложим последовательно п равных отрезков АА1, А1А2, …. Ан-14, (рис. 167), т. е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (на рисунке 167 n = 5). Проведём прямую А„В (точка А, — конец последнего отрезка) и построим прямые, проходящие через точки А1, А2, … , Аn-1 и параллельные прямой А,В. Эти прямые пересекают отрезок АВ в точках В1, В2, … , В1 — 1, которые по теореме Фалеса (задача 385) делят отрезок АВ на п равных частей.

Дано: острый угол hk и два отрезка P1Q1 и P2Q2. Требуется построить параллелограмм ABCD так, чтобы расстояние между параллельными прямыми AB и DC равнялось P1Q1, AB = P2Q2 и угол A = углу hk.

Решение:
1. Построим прямую а, отметим точку А и отложим отрезок AB = P2Q2.
2. Проведем окружности для построения точки Е, через которую проведем прямую b, образующую угол hk с прямой а.
3. Восстановим перпендикуляр к прямой а в точке А, затем в точке Н, получив прямую d.
4. Найдем точку D как пересечение прямых b и d.
5. Проведем окружность с центром в точке В и радиусом AD, найдя точку С.
6. Соединим точки А, В, С и D, получив параллелограмм ABCD.
7. Проверим, что расстояние между AB и DC равно P1Q1.

Параллелограмм ABCD построен с заданными параметрами.

Дано: острый угол hk и два отрезка P1Q1 и P2Q2. Требуется построить параллелограмм ABCD так, чтобы расстояние между параллельными прямыми AB и DC равнялось P1Q1, AB = P2Q2 и угол A = углу hk.

Решение:

1. Построим прямую а и отметим на ней точку А. Отложим отрезок AB = P2Q2.
2. Проведем окружность с центром в точке А и радиусом AF, затем окружность с центром в точке F и радиусом EF. Точка пересечения — точка Е.
3. Через точки А и Е проведем прямую b, образующую с прямой а угол hk.
4. Восстановим перпендикуляр к прямой а в точке А. Для этого проведем окружность с центром в точке А и произвольным радиусом, затем окружность с центром в точке О и радиусом ON. Пересечение — точка Н.
5. Восстановим перпендикуляр к прямой а в точке Н. Проведем окружность с центром в точке Н и произвольным радиусом, затем окружность с центром в точке М и радиусом РМ. Пересечение — точка W.
6. Через точки Н и W проведем прямую d. Пересечение прямой d с прямой b — точка D.
7. Проведем окружность с центром в точке В и радиусом AD. Пересечение с прямой d — точка С.
8. Соединим точки А, В, С и D, получив параллелограмм ABCD.
9. Проверим, что расстояние между AB и DC равно P1Q1.
10. Параллелограмм ABCD построен с заданными параметрами.

Каждый шаг выполняется последовательно, с использованием циркуля и линейки, чтобы обеспечить точность построения.