
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 394 Атанасян — Подробные Ответы
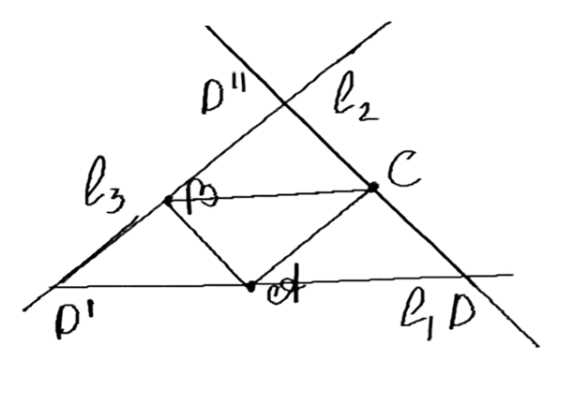
Даны три точки А, В и С, не лежащие на одной прямой. Постройте параллелограмм так, чтобы три его вершины совпадали с данными точками. Сколько таких параллелограммов можно построить?
Можно построить три параллелограмма. Точки А, В и С фиксированы, а точка D может изменяться, создавая три различных варианта параллелограмма. Это возможно, так как для каждого из трёх случаев точка D выбирается так, чтобы выполнялись условия параллелограмма.
Даны три точки А, В и С, не лежащие на одной прямой. Необходимо построить параллелограмм так, чтобы три его вершины совпадали с данными точками.
Рассмотрим решение задачи.
1. Параллелограмм определяется двумя парами параллельных сторон. Это означает, что для построения параллелограмма нужно, чтобы противоположные стороны были равны и параллельны.
2. Точки А, В и С фиксированы. Четвёртая точка D должна быть выбрана так, чтобы выполнялись условия параллелограмма.
3. Рассмотрим три возможных случая:
— Если точки А и В являются вершинами одной стороны, а точка С — вершиной смежной стороны, то точка D должна быть такой, чтобы вектор AD был равен вектору BC. Это даёт первый параллелограмм.
— Если точки А и С являются вершинами одной стороны, а точка В — вершиной смежной стороны, то точка D должна быть такой, чтобы вектор AD был равен вектору CB. Это даёт второй параллелограмм.
— Если точки В и С являются вершинами одной стороны, а точка А — вершиной смежной стороны, то точка D должна быть такой, чтобы вектор BD был равен вектору CA. Это даёт третий параллелограмм.
4. Таким образом, можно построить три различных параллелограмма, так как точка D может быть выбрана тремя разными способами, удовлетворяющими условиям параллелограмма.
5. Каждый из этих параллелограммов будет иметь три вершины, совпадающие с точками А, В и С, а четвёртая вершина будет определяться в зависимости от выбора точки D.
6. Это решение учитывает все возможные варианты построения параллелограмма при заданных условиях и демонстрирует, что таких вариантов может быть ровно три.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!