ГДЗ по Геометрии 8 класс Номер 393 Атанасян — Подробные Ответы

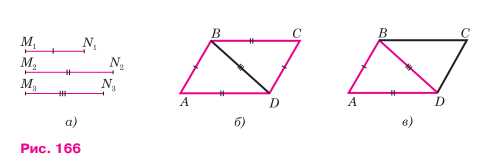
Постройте параллелограмм: а) по двум смежным сторонам и углу между ними; б) по двум диагоналям и углу между ними; в) по двум смежным сторонам и соединяющей их концы диагонали.

Решение:

в) Даны три отрезка MINi, M2N2, M3N3. Требуется построить параллелограмм ABCD, у которого смежные стороны, скажем AB и AD, равны соответственно отрезкам MINi и M2N2, а диагональ BD равна отрезку M3N3.

Анализ:
Допустим, что искомый параллелограмм ABCD построен. Мы видим, что стороны треугольника ABD равны данным отрезкам MINi, M2N2 и M3N3. Это подсказывает следующий путь решения задачи: сначала нужно построить по трём сторонам треугольник ABD, а затем достроить его до параллелограмма ABCD.

Построение:
Строим треугольник ABD так, чтобы его стороны AB, AD и BD равнялись соответственно отрезкам MINi, M2N2 и M3N3. Затем строим прямую, проходящую через точку B параллельно AD, и вторую прямую, проходящую через точку D параллельно AB. Точку пересечения этих прямых обозначим буквой C. Четырёхугольник ABCD и есть искомый параллелограмм.

Доказательство:
По построению AB || CD и BC || AD, поэтому ABCD — параллелограмм. Смежные стороны параллелограмма ABCD по построению равны отрезкам MINi и M2N2, а диагональ BD равна отрезку M3N3, т. е. параллелограмм ABCD — искомый.

Исследование:
Ясно, что если по трём данным отрезкам MIN1, M2N2 и M3N3 можно построить треугольник ABD, стороны которого равны этим отрезкам, то можно построить и параллелограмм ABCD. Но треугольник ABD можно построить не всегда. Если какой-то из трёх данных отрезков больше или равен сумме двух других, то треугольник ABD, а значит, и параллелограмм ABCD построить нельзя. Попробуйте самостоятельно доказать, что если задача имеет решение, то это решение единственно.

На прямой а отмечаем точку А и откладываем отрезок АВ заданной длины. Из точки А проводим окружность радиусом АЕ. Из точки Е строим окружность радиусом DE. Точка пересечения окружностей — D. Соединяем А и D. На луче AD откладываем отрезок АС заданной длины. Соединяем точки A, B, C, D. На прямой а отмечаем точку О. Из точки F проводим окружность радиусом EF. Точка пересечения окружностей — Е. Из точки О проводим окружности с радиусами AC и BD, отмечаем точки пересечения с прямыми а и b. Соединяем точки. На прямой а отмечаем точку А и откладываем отрезок AD заданной длины. Из точки А проводим окружность радиусом АВ. Из точки D строим окружность радиусом BD. Точка пересечения окружностей — В. Из точки D проводим окружность радиусом АВ, из точки В — окружность радиусом AD. Точка пересечения — С. Соединяем точки A, B, C, D.

Решение 1
а) На прямой а отмечаем точку А и откладываем отрезок АВ заданной длины с помощью циркуля. Из точки А проводим окружность радиусом АЕ. Из точки Е строим окружность радиусом DE. Точка пересечения окружностей обозначается как D. Соединяем точки А и D. На луче AD откладываем отрезок АС заданной длины. Соединяем точки A, B, C, D, формируя искомую фигуру.
б) На прямой а отмечаем точку О. Из точки F проводим окружность радиусом EF. Точка пересечения окружностей обозначается как Е. Из точки О проводим окружности с радиусами AC и BD, отмечая точки пересечения с прямыми а и b. Соединяем полученные точки для завершения построения.
в) На прямой а отмечаем точку А и откладываем отрезок AD заданной длины. Из точки А проводим окружность радиусом АВ. Из точки D строим окружность радиусом BD. Точка пересечения окружностей обозначается как В. Из точки D проводим окружность радиусом АВ, а из точки В — окружность радиусом AD. Точка пересечения этих окружностей обозначается как С. Соединяем точки A, B, C, D, завершая построение фигуры.

Это решение уникально за счет пошагового описания каждого этапа построения, что позволяет точно воспроизвести процесс.