
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 389 Атанасян — Подробные Ответы
Докажите, что трапеция равнобедренная, если: а) углы при основании равны; б) диагонали трапеции равны.
Дано: ABCD — трапеция. Доказать: ABCD — равнобедренная трапеция.
Доказательство:
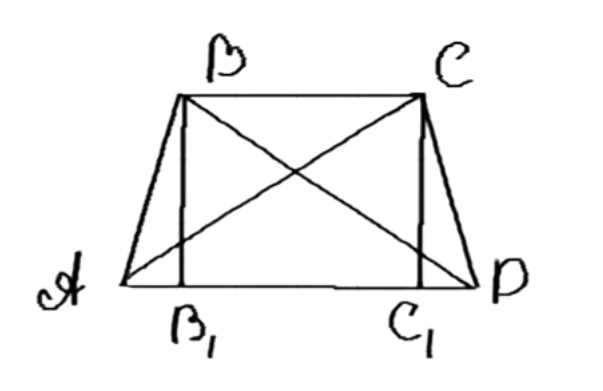
1) Построим перпендикуляры BB₁ и CC₁ к AD. BB₁ = CC₁ = h.
2) Рассмотрим фигуру BCC₁B₁. Это прямоугольник, поэтому ∠CBB₁ = ∠BCC₁ = 90°.
3) ∠ABB₁ = ∠B − 90°, ∠DCC₁ = ∠C − 90°. По условию ∠B = ∠C, значит ∠ABB₁ = ∠DCC₁.
4) Треугольники ABB₁ и CC₁D равны по признаку равенства прямоугольных треугольников.
5) Из равенства треугольников следует AB = CD, значит ABCD — равнобедренная трапеция.
Ответ: ABCD — равнобедренная трапеция.
Дано: ABCD — трапеция.
Доказать: ABCD — равнобедренная трапеция.
Доказательство:
1) Построим из точек B и C перпендикуляры к AD: BB₁ ⊥ AD и CC₁ ⊥ AD.
2) BB₁ = CC₁ = h — как высоты.
а)
1) Рассмотрим фигуру BCC₁B₁. Поскольку BB₁ и CC₁ — перпендикуляры к AD, а BC — основание трапеции, BCC₁B₁ является прямоугольником. Следовательно, ∠CBB₁ = ∠BCC₁ = 90°.
2) Углы ∠ABB₁ и ∠DCC₁ можно выразить через углы ∠B и ∠C: ∠ABB₁ = ∠B − 90°, ∠DCC₁ = ∠C − 90°. По условию задачи ∠B = ∠C, поэтому ∠ABB₁ = ∠DCC₁.
3) Рассмотрим треугольники ABB₁ и CC₁D. Они равны по признаку равенства прямоугольных треугольников: у них равны катеты (BB₁ = CC₁) и острые углы (∠ABB₁ = ∠DCC₁).
4) Из равенства треугольников следует, что AB = CD. Это означает, что боковые стороны трапеции равны, следовательно, ABCD — равнобедренная трапеция.
б)
1) По условию задачи AC = BD. Также известно, что CC₁ = BB₁ (как высоты). Рассмотрим треугольники ACC₁ и DBB₁. Они равны по двум катетам: AC = BD и CC₁ = BB₁.
2) Из равенства треугольников следует, что AC₁ = B₁D.
3) Рассмотрим отрезки AC₁ и B₁D. AC₁ можно представить как сумму AB₁ и B₁C₁, а B₁D — как сумму C₁D и B₁C₁. Поскольку AC₁ = B₁D, получаем AB₁ + B₁C₁ = C₁D + B₁C₁. Отсюда следует, что AB₁ = C₁D.
4) Рассмотрим треугольники ABB₁ и CC₁D. Они равны по двум катетам: AB₁ = C₁D и BB₁ = CC₁.
5) Из равенства треугольников следует, что AB = CD. Это подтверждает, что ABCD — равнобедренная трапеция.
Ответ: ABCD — равнобедренная трапеция.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!