
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 385 Атанасян — Подробные Ответы
Докажите теорему Фалеса1: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вто- рую прямую, то они отсекут на второй прямой равные между собой отрезки.
Решение
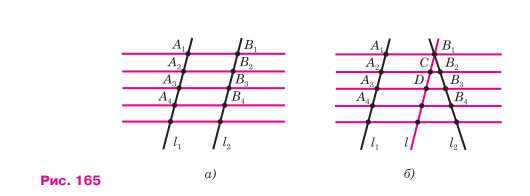
Пусть на прямой И отложены равные отрезки A1A2, A2A3, A3A4, … и через их концы проведены параллельные прямые, которые пересекают прямую [2 в точках B1, B2, B3, B4, … (рис. 165). Требуется доказать, что отрезки B1B2, B2B3, B2B4, … равны друг другу. Докажем, например, что B1B2 = B2B3. Рассмотрим сначала случай, когда прямые 11 и 12 параллельны (рис. 165, а). Тогда A1 A2 = B1B2 и A2A3 = B2B3 как противопо- ложные стороны параллелограммов A1B1B2A2 и A2B2B3A3. Так как A1 A2 = A2 A3, то и B1B2 =B2B3. Если прямые 11 и 12 не па- раллельны, то через точку В1 проведём прямую 1, параллель- ную прямой 11 (рис. 165, б). Она пересечёт прямые A2 B2 и A3B3 в некоторых точках С и D. Так как A1A2 = A2A3, то по дока- занному B1C = CD. Отсюда получаем: B1B2 = B2B3 (задача 384). Аналогично можно доказать, что В В = В.В. и т. д.
Пусть на прямой l₁ отложены равные отрезки A₁A₂, A₂A₃, A₃A₄ и так далее. Через их концы проведены параллельные прямые, пересекающие прямую l₂ в точках B₁, B₂, B₃, B₄ и так далее. Требуется доказать, что отрезки B₁B₂, B₂B₃, B₃B₄ и так далее равны друг другу.
Если прямые l₁ и l₂ параллельны, то A₁A₂ = B₁B₂ и A₂A₃ = B₂B₃ как противоположные стороны параллелограммов A₁B₁B₂A₂ и A₂B₂B₃A₃. Так как A₁A₂ = A₂A₃, то и B₁B₂ = B₂B₃.
Если прямые l₁ и l₂ не параллельны, то через точку B₁ проведем прямую, параллельную прямой l₁. Она пересечет прямые A₂B₂ и A₃B₃ в точках C и D. Так как A₁A₂ = A₂A₃, то B₁C = CD. Отсюда B₁B₂ = B₂B₃.
Аналогично доказывается равенство остальных отрезков. Таким образом, все отрезки на прямой l₂ равны.
Решение задачи:
1) Пусть на прямой l₁ отложены равные отрезки: A₁A₂, A₂A₃, A₃A₄ и так далее. Через их концы проведены параллельные прямые, которые пересекают прямую l₂ в точках B₁, B₂, B₃ и так далее. Необходимо доказать, что B₁B₂ = B₂B₃ = B₃B₄ = …
2) Рассмотрим первый случай, когда прямые l₁ и l₂ параллельны.
а) Если l₁ || l₂, то отрезки A₁A₂ и B₁B₂, а также A₂A₃ и B₂B₃ являются противоположными сторонами параллелограмма.
б) Поскольку A₁A₂ = A₂A₃ (по условию), то B₁B₂ = B₂B₃.
3) Рассмотрим второй случай, когда прямые l₁ и l₂ не параллельны.
а) Проведем через точку B₁ прямую, параллельную l₁. Обозначим точки пересечения этой прямой с A₂B₂ и A₃B₃ как C и D соответственно.
б) Так как A₁A₂ = A₂A₃ (по условию), то отрезки B₁C и CD также равны.
в) Из равенства B₁C = CD следует, что B₁B₂ = B₂B₃ (по задаче 384).
4) Таким образом, в обоих случаях доказано, что отрезки на прямой l₂ равны: B₁B₂ = B₂B₃ = B₃B₄ = …
Это полное решение задачи с детализацией каждого шага.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!