
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 384 Атанасян — Подробные Ответы
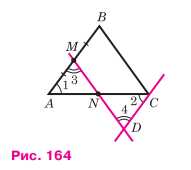
Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.
Решение задачи:
Через точку С проведём прямую, параллельную прямой АВ, и обозначим буквой D точку пересечения этой прямой с прямой MN. Так как АМ = МВ по условию, а MB = CD как противоположные стороны параллелограмма BCDM, то AM = DC. Треугольники AMN и CDN равны по второму признаку равенства треугольников (AM = CD, ∠1 = ∠2 и ∠3 = ∠4 как накрест лежащие углы при пересечении параллельных прямых AB и CD секущими AC и MD), поэтому AN = NC.
Дано: ABC — треугольник, AM = MB, ME ⊥ AB, MD || BC, MD ∩ AC = N.
Доказать: AN = NC.
Решение:
1. Проведем через C прямую, параллельную AB, и обозначим ее пересечение с MN как D.
2. Четырехугольник MBCD — параллелограмм, так как MD || BC и MB || CD.
3. Из свойств параллелограмма MB = CD. Учитывая AM = MB, получаем AM = CD.
4. Углы ∠3 = ∠4 и ∠1 = ∠2 как накрест лежащие при параллельных прямых MD и BC.
5. Треугольники AMN и CDN равны по стороне (AM = CD) и двум углам (∠1 = ∠2, ∠3 = ∠4).
6. Из равенства треугольников следует AN = NC.
Доказано.
Дано: ABC — треугольник, AM = MB, ME ⊥ AB, MD || BC, MD ∩ AC = N.
Доказать: AN = NC.
Доказательство:
1. Проведем прямую, параллельную AB, через точку C. Обозначим точку пересечения этой прямой с MN как D.
2. Рассмотрим четырехугольник MBCD. Поскольку MD || BC (по условию) и MB || CD (по построению), MBCD является параллелограммом.
3. В параллелограмме противоположные стороны равны. Следовательно, MB = CD. Учитывая, что AM = MB (по условию), получаем AM = CD.
4. Рассмотрим углы, образованные при пересечении прямых. Углы ∠3 и ∠4 равны как накрест лежащие при параллельных прямых MD и BC и секущей AC. Аналогично, углы ∠1 и ∠2 равны как накрест лежащие при параллельных прямых MD и BC и секущей AB.
5. Рассмотрим треугольники AMN и CDN. В них:
— AM = CD (из пункта 3),
— ∠1 = ∠2 (из пункта 4),
— ∠3 = ∠4 (из пункта 4).
Следовательно, треугольники AMN и CDN равны по стороне и двум прилежащим углам.
6. Из равенства треугольников следует, что соответствующие элементы равны. В частности, AN = NC.
Таким образом, доказано, что AN = NC.
Это полное решение с детализацией каждого шага, включая построение, анализ фигур и доказательство равенства отрезков.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!