ГДЗ по Геометрии 8 класс Номер 383 Атанасян — Подробные Ответы

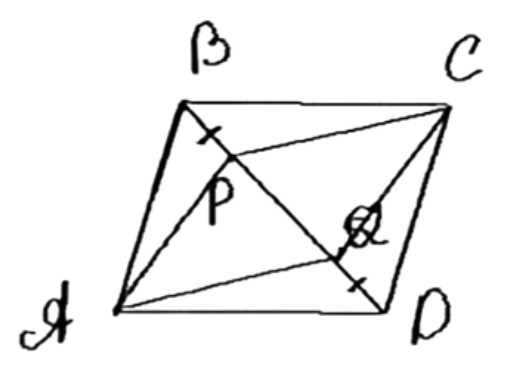
На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что PB = QD. Докажите, что четырёхугольник APCQ — параллелограмм.

Краткое решение:

Дано: ABCD — параллелограмм, BD — диагональ, точки P и E лежат на BD, PB = QD.

1. Рассмотрим треугольники ABP и CDQ: AB = CD, PB = QD, угол ABP = угол CDQ (накрест лежащие). Следовательно, треугольники равны, и AP = CQ.

2. Рассмотрим треугольники CBP и ADQ: BC = AD, PB = QD, угол CBP = угол ADQ (накрест лежащие). Следовательно, треугольники равны, и CP = AQ.

3. В четырехугольнике APCQ противоположные стороны равны: AP = CQ и CP = AQ.

4. По второму признаку параллелограмма, APCQ — параллелограмм.

Доказано.

Полное решение задачи с детализацией:

Дано: ABCD — параллелограмм, BD — диагональ, точки P и E лежат на BD, причем PB = QD.
Доказать: APCQ — параллелограмм.

Доказательство:

1. По свойству параллелограмма, противоположные стороны равны и параллельны: AB = CD, BC = AD, AB || CD, BC || AD.

2. Рассмотрим треугольники ABP и CDQ:
— AB = CD (по свойству параллелограмма),
— PB = QD (по условию),
— Угол ABP равен углу CDQ, так как они являются накрест лежащими при параллельных прямых AB и CD и секущей BD.
Следовательно, треугольники ABP и CDQ равны по двум сторонам и углу между ними.

3. Рассмотрим треугольники CBP и ADQ:
— BC = AD (по свойству параллелограмма),
— PB = QD (по условию),
— Угол CBP равен углу ADQ, так как они являются накрест лежащими при параллельных прямых BC и AD и секущей BD.
Следовательно, треугольники CBP и ADQ равны по двум сторонам и углу между ними.

4. Из равенства треугольников ABP и CDQ следует, что AP = CQ.
Из равенства треугольников CBP и ADQ следует, что CP = AQ.

5. В четырехугольнике APCQ противоположные стороны равны: AP = CQ и CP = AQ.

6. По второму признаку параллелограмма, если в четырехугольнике противоположные стороны равны, то он является параллелограммом.

Вывод: APCQ — параллелограмм.

Доказательство завершено.