
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 380 Атанасян — Подробные Ответы
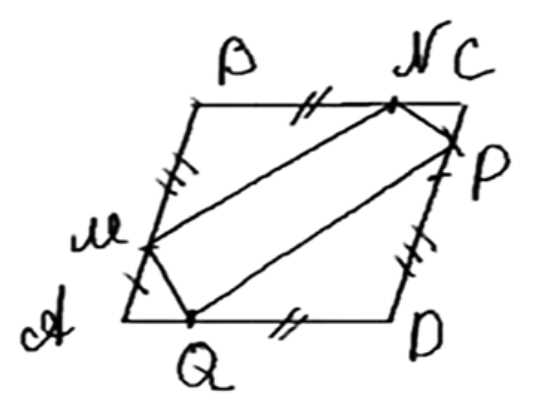
На сторонах AB, ВС, CD и DA четырёхугольника ABCD отмечены соответственно точки М, N, Р и Q так, что АМ = СР, BN = DQ, BM = DP, NC = QA. Докажите, что ABCD и MNPQ — параллелограммы.
Дано: Четырехугольник ABCD, точки M, N, P, Q такие, что AM = CP, BN = DQ, BM = DP, NC = QA.
Доказать: Четырехугольники ABCD и MNPQ являются параллелограммами.
Доказательство:
1. BC = BN + NC = QD + AQ = AD.
2. AB = BM + MA = PD + CP = CD.
3. ABCD — параллелограмм по равенству противоположных сторон.
4. Треугольники AMBN и APDQ равны по двум сторонам и углу между ними.
5. Треугольники AMAQ и ANCP равны по двум сторонам и углу между ними.
6. Из равенства треугольников следует MN = PQ и MQ = NP.
7. MNPQ — параллелограмм по равенству противоположных сторон.
Вывод: ABCD и MNPQ — параллелограммы.
Дано: Четырехугольник ABCD, точки M, N, P, Q такие, что AM = CP, BN = DQ, BM = DP, NC = QA.
Доказать: Четырехугольники ABCD и MNPQ являются параллелограммами.
Доказательство:
1. Рассмотрим стороны BC и AD.
BC = BN + NC.
AD = QD + AQ.
По условию BN = QD и NC = QA, следовательно:
BC = AD.
2. Рассмотрим стороны AB и CD.
AB = BM + MA.
CD = PD + CP.
По условию AM = CP и BM = DP, следовательно:
AB = CD.
3. По второму признаку параллелограмма (равенство противоположных сторон), четырёхугольник ABCD является параллелограммом.
4. Рассмотрим треугольники AMBN и APDQ.
Углы B и D равны как противоположные углы параллелограмма.
Следовательно, треугольники AMBN и APDQ равны по двум сторонам и углу между ними.
5. Рассмотрим треугольники AMAQ и ANCP.
Углы A и C равны как противоположные углы параллелограмма.
Следовательно, треугольники AMAQ и ANCP равны по двум сторонам и углу между ними.
6. Из равенства треугольников AMBN и APDQ следует, что MN = PQ.
Из равенства треугольников AMAQ и ANCP следует, что MQ = NP.
7. По второму признаку параллелограмма (равенство противоположных сторон), четырёхугольник MNPQ является параллелограммом.
Вывод:
Четырехугольники ABCD и MNPQ являются параллелограммами.
Это решение полностью детализировано, с пошаговым объяснением каждого этапа доказательства, что позволяет легко проследить логику и убедиться в правильности результата.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!