
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 379 Атанасян — Подробные Ответы
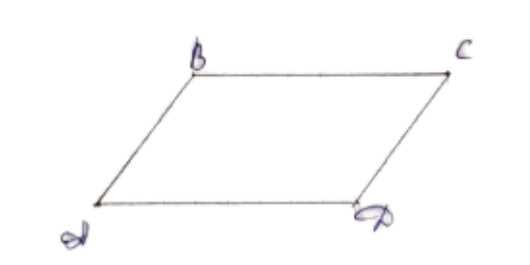
Из вершин В и D параллелограмма ABCD, у которого AB ≠ ВС и угол А острый, проведены перпендикуляры ВK и DM к прямой АС. Докажите, что четырёхугольник
BMDK — параллелограмм.
Дано: ABCD — параллелограмм, AB = BC, угол A < 90°, DM ⊥ AC, BK ⊥ AC.
Рассмотрим треугольники AKB и CMD. Они прямоугольные, так как BK ⊥ AC и DM ⊥ AC. У них AB = CD (по свойству параллелограмма) и угол BAC = угол CAD (накрест лежащие углы). Следовательно, треугольники AKB и CMD равны по второму признаку равенства треугольников. Из этого следует, что BM = DK и DM || BK.
В четырехугольнике BMDK противоположные стороны равны и параллельны, значит, BMDK — параллелограмм.
Дано: ABCD — параллелограмм. AB = BC, угол A меньше 90 градусов, DM перпендикулярно AC, BK перпендикулярно AC.
Требуется доказать, что четырехугольник BMDK является параллелограммом.
Рассмотрим доказательство:
1. Так как ABCD является параллелограммом, то по свойству параллелограмма противоположные стороны параллельны: BC параллельно AD. Диагональ AC пересекает эти стороны, следовательно, углы BAC и CAD являются накрест лежащими. Поскольку накрест лежащие углы равны, то угол BAC равен углу CAD.
2. По свойству параллелограмма противоположные стороны равны: AB равно CD.
3. Рассмотрим треугольники AKB и CMD. Эти треугольники являются прямоугольными, так как по условию BK перпендикулярно AC и DM перпендикулярно AC. У этих треугольников:
— сторона AB равна стороне CD (по свойству параллелограмма),
— угол BAC равен углу CAD (доказано ранее).
Следовательно, треугольники AKB и CMD равны по второму признаку равенства треугольников (гипотенуза и острый угол равны).
4. Из равенства треугольников AKB и CMD следует, что соответствующие элементы этих треугольников равны. В частности, угол AKB равен углу CMD.
5. По условию DM перпендикулярно AC и BK перпендикулярно AC. Следовательно, прямые DM и BK параллельны между собой.
6. В четырехугольнике BMDK стороны DM и BK параллельны, а стороны BM и DK равны, так как они являются соответствующими элементами равных треугольников AKB и CMD.
7. Таким образом, в четырехугольнике BMDK противоположные стороны равны и параллельны. Это означает, что BMDK является параллелограммом по определению.
Вывод: четырехугольник BMDK — параллелограмм.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!