
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 377 Атанасян — Подробные Ответы
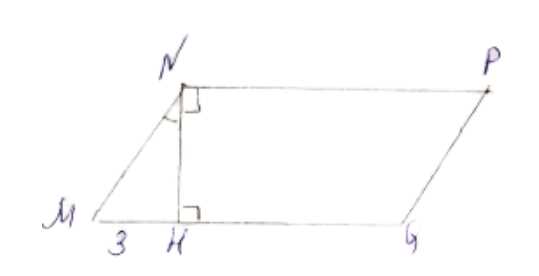
В параллелограмме MNPQ проведён перпендикуляр NH к прямой MQ, причём точка Н лежит на стороне MQ. Найдите стороны и углы параллелограмма, если известно, что МН = 3 см, HQ = 5 см, ∠MNH = 30°.
Дано: ABCD — параллелограмм. NH ⊥ MQ. MH = 3 см, HQ = 5 см, ∠MNH = 30°. Найти углы M, N, LP, LQ и стороны MN, NP, PQ, MQ.
Решение:
1. В треугольнике MNH, который прямоугольный, MN = 2 × MH = 6 см (по свойству треугольника с углом 30°).
2. MQ = MN + HQ = 6 см + 5 см = 8 см.
3. Угол NMH = 90° — 30° = 60°, значит, ∠M = 60°.
4. Угол N = 180° — ∠M = 120° (по свойству параллелограмма).
5. По свойствам параллелограмма: ∠LP = ∠M = 60°, ∠LQ = ∠N = 120°, MN = PQ = 6 см, MQ = NP = 8 см.
Ответ: ∠M = ∠LP = 60°, ∠N = ∠LQ = 120°, MN = PQ = 6 см, MQ = NP = 8 см.
Дано: ABCD — параллелограмм. Прямая NH перпендикулярна MQ. MH = 3 см, HQ = 5 см, угол MNH = 30°. Требуется найти: углы M, N, LP, LQ, а также стороны MN, NP, PQ, MQ.
Решение:
1. По условию задачи четырехугольник MNPQ является параллелограммом. Это следует из того, что противоположные стороны параллельны и равны. Тогда по свойствам параллелограмма:
— Углы M и LP равны, то есть ∠M = ∠LP.
— Углы N и LQ равны, то есть ∠N = ∠LQ.
— Противоположные стороны равны, то есть MN = PQ и NP = MQ.
2. Рассмотрим треугольник MNH. Он прямоугольный, так как NH перпендикулярна MQ. В этом треугольнике угол MNH равен 30°. По свойству прямоугольного треугольника с углом 30° катет, лежащий напротив угла 30°, равен половине гипотенузы. Следовательно,
MN = 2 × MH = 2 × 3 см = 6 см.
Таким образом, MN = PQ = 6 см.
3. Найдем длину стороны MQ. По условию, MQ состоит из отрезков MN и HQ, то есть
MQ = MN + HQ = 6 см + 5 см = 8 см.
Следовательно, MQ = NP = 8 см.
4. Найдем угол NMH. В треугольнике MNH угол NMH равен разности между прямым углом (90°) и углом MNH.
∠NMH = 90° — ∠MNH = 90° — 30° = 60°.
Так как угол NMH равен углу M (по свойству параллелограмма), то
∠M = 60°.
5. Найдем угол N. Углы M и N являются односторонними, так как они лежат на одной стороне параллельных прямых MN и PQ. Сумма односторонних углов равна 180°.
∠M + ∠N = 180°.
Подставим значение угла M:
60° + ∠N = 180°.
∠N = 180° — 60° = 120°.
Таким образом, ∠N = 120°.
6. Так как углы N и LQ равны (по свойству параллелограмма), то
∠LQ = 120°.
А углы M и LP равны, то
∠LP = 60°.
Ответ:
∠M = ∠LP = 60°, ∠N = ∠LQ = 120°, MN = PQ = 6 см, MQ = NP = 8 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!