
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 376 Атанасян — Подробные Ответы
Найдите углы параллелограмма ABCD, если:
а) ∠A = 84°; б) ∠A − ∠B = 55°; в) ∠A + ∠C = 142°; г) ∠A = 2∠B; д) ∠CAD = 16°, ∠ACD = 37°.
а) ∠A = 84°. В параллелограмме ∠A + ∠B = 180°. ∠B = 180° — 84° = 96°. Ответ: ∠A = ∠C = 84°, ∠B = ∠D = 96°.
б) ∠A — ∠B = 55°. ∠A = ∠B + 55°. ∠A + ∠B = 180°. (∠B + 55°) + ∠B = 180°. 2∠B = 125°. ∠B = 62°30′. ∠A = 117°30′. Ответ: ∠A = ∠C = 117°30′, ∠B = ∠D = 62°30′.
в) ∠A + ∠C = 142°. ∠A = ∠C, поэтому 2∠A = 142°. ∠A = 71°. ∠B = 180° — ∠A = 109°. Ответ: ∠A = ∠C = 71°, ∠B = ∠D = 109°.
г) ∠A = 2∠B. ∠A + ∠B = 180°. 2∠B + ∠B = 180°. 3∠B = 180°. ∠B = 60°. ∠A = 120°. Ответ: ∠A = ∠C = 120°, ∠B = ∠D = 60°.
д) ∠CAD = 16°, ∠ACD = 37°. В треугольнике ACD: ∠ACD + ∠CDA + ∠DAC = 180°. 37° + 16° + ∠CDA = 180°. ∠CDA = 127°. ∠D = ∠B = 127°. ∠A = 180° — ∠D = 53°. Ответ: ∠A = ∠C = 53°, ∠B = ∠D = 127°.
Дано: ABCD — параллелограмм.
a) ∠A = 84°.
б) ∠A — ∠B = 55°.
в) ∠A + ∠C = 142°.
г) ∠A = 2∠B.
д) ∠CAD = 16°, ∠ACD = 37°.
Найти: ∠A, ∠B, ∠C, ∠D.
Решение:
1. По свойствам параллелограмма противоположные углы равны, то есть ∠A = ∠C, ∠B = ∠D. Также сумма углов, лежащих на одной стороне, равна 180°.
а) Дано: ∠A = 84°.
Из свойства параллелограмма следует, что ∠A + ∠B = 180°. Подставим значение:
84° + ∠B = 180°.
Вычтем 84° из обеих частей уравнения:
∠B = 180° — 84°.
∠B = 96°.
Так как ∠B = ∠D, а ∠A = ∠C, то получаем:
∠A = 84°, ∠C = 84°, ∠B = 96°, ∠D = 96°.
б) Дано: ∠A — ∠B = 55°.
Из условия следует, что ∠A = ∠B + 55°. Подставим это в уравнение ∠A + ∠B = 180°:
(∠B + 55°) + ∠B = 180°.
Сложим одинаковые члены:
2∠B + 55° = 180°.
Вычтем 55° из обеих сторон уравнения:
2∠B = 180° — 55°.
2∠B = 125°.
Разделим обе стороны на 2:
∠B = 125° / 2.
∠B = 62,5° или 62°30′.
Теперь найдем ∠A:
∠A = ∠B + 55°.
∠A = 62°30′ + 55°.
∠A = 117°30′.
Так как ∠A = ∠C, а ∠B = ∠D, то:
∠A = 117°30′, ∠C = 117°30′, ∠B = 62°30′, ∠D = 62°30′.
в) Дано: ∠A + ∠C = 142°.
Так как ∠A = ∠C, то можно записать:
2∠A = 142°.
Разделим обе стороны на 2:
∠A = 142° / 2.
∠A = 71°.
Теперь найдем ∠B:
∠A + ∠B = 180°.
71° + ∠B = 180°.
Вычтем 71° из обеих сторон:
∠B = 180° — 71°.
∠B = 109°.
Так как ∠A = ∠C, а ∠B = ∠D, то:
∠A = 71°, ∠C = 71°, ∠B = 109°, ∠D = 109°.
г) Дано: ∠A = 2∠B.
Подставим это в уравнение ∠A + ∠B = 180°:
2∠B + ∠B = 180°.
Сложим одинаковые члены:
3∠B = 180°.
Разделим обе стороны на 3:
∠B = 180° / 3.
∠B = 60°.
Теперь найдем ∠A:
∠A = 2∠B.
∠A = 2 × 60°.
∠A = 120°.
Так как ∠A = ∠C, а ∠B = ∠D, то:
∠A = 120°, ∠C = 120°, ∠B = 60°, ∠D = 60°.
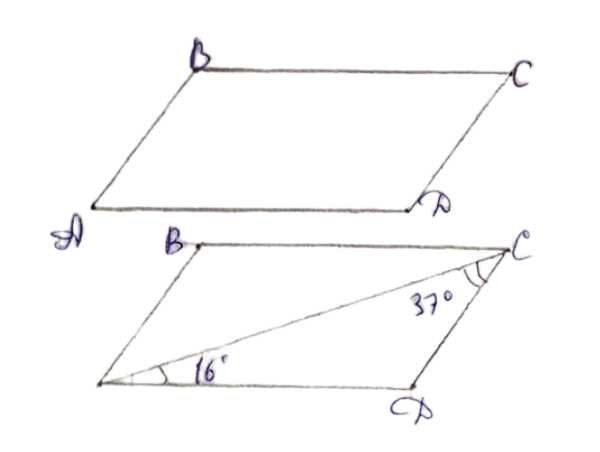
д) Дано: ∠CAD = 16°, ∠ACD = 37°.
В треугольнике сумма углов равна 180°. Рассмотрим треугольник ACD:
∠ACD + ∠CDA + ∠DAC = 180°.
Подставим известные значения:
37° + 16° + ∠CDA = 180°.
Сложим известные углы:
53° + ∠CDA = 180°.
Вычтем 53° из обеих сторон:
∠CDA = 180° — 53°.
∠CDA = 127°.
Так как ∠CDA является частью угла ∠D, а ∠D = ∠B, то:
∠D = 127°, ∠B = 127°.
Теперь найдем ∠A:
∠A + ∠B = 180°.
∠A + 127° = 180°.
Вычтем 127° из обеих сторон:
∠A = 180° — 127°.
∠A = 53°.
Так как ∠A = ∠C, то:
∠A = 53°, ∠C = 53°, ∠B = 127°, ∠D = 127°.
Ответ:
а) ∠A = 84°, ∠B = 96°, ∠C = 84°, ∠D = 96°.
б) ∠A = 117°30′, ∠B = 62°30′, ∠C = 117°30′, ∠D = 62°30′.
в) ∠A = 71°, ∠B = 109°, ∠C = 71°, ∠D = 109°.
г) ∠A = 120°, ∠B = 60°, ∠C = 120°, ∠D = 60°.
д) ∠A = 53°, ∠B = 127°, ∠C = 53°, ∠D = 127°.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!