
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 363 Атанасян — Подробные Ответы
Начертите выпуклые пятиугольник и шестиугольник. В каждом многоугольнике из какой-нибудь вершины проведите все диагонали. На сколько треугольников разделяют проведённые диагонали каждый многоугольник?
Строим выпуклый шестиугольник и пятиугольник. Из одной вершины каждого многоугольника проводим все возможные диагонали. В шестиугольнике диагонали делят его на 4 треугольника, в пятиугольнике на 3 треугольника. Ответ: 4 и 3.
1. Начнем с построения выпуклых многоугольников. Сначала чертим правильный шестиугольник, а затем правильный пятиугольник. Выпуклость означает, что все углы многоугольников меньше 180 градусов, а все вершины находятся «снаружи» фигуры.
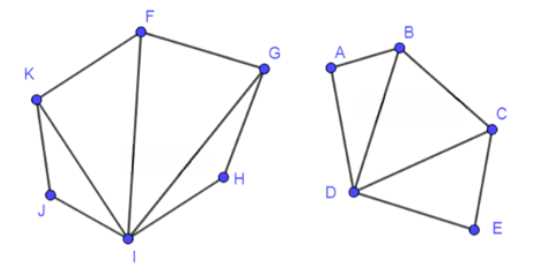
2. Выберем одну вершину в каждом из многоугольников. В шестиугольнике, например, обозначим эту вершину как F, а в пятиугольнике — как A. Из этих вершин проведем все возможные диагонали, то есть линии, соединяющие выбранную вершину с другими вершинами, кроме соседних.
3. В шестиугольнике из вершины F можно провести четыре диагонали, так как шестиугольник имеет шесть вершин, и две из них являются соседними (их соединение не является диагональю). Эти диагонали делят шестиугольник на четыре треугольника.
4. В пятиугольнике из вершины A можно провести три диагонали, так как пятиугольник имеет пять вершин, и две из них также являются соседними. Эти диагонали делят пятиугольник на три треугольника.
5. После построения диагоналей подсчитаем количество образовавшихся треугольников. В шестиугольнике их четыре, а в пятиугольнике — три.
Ответ: в шестиугольнике получается 4 треугольника, а в пятиугольнике — 3 треугольника.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!