ГДЗ по Геометрии 7 класс Номер 55 Атанасян — Подробные Ответы

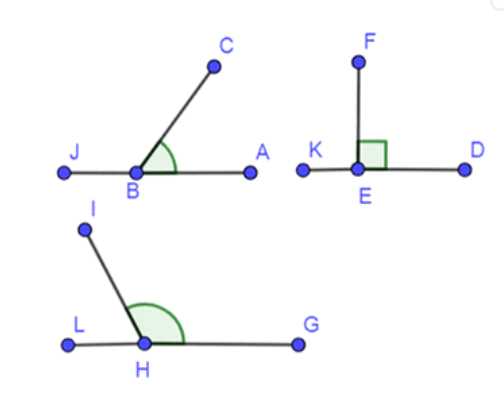
Начертите три угла: острый, прямой и тупой. Для каждого из них начертите смежный угол.

Начертим три угла: острый, прямой и тупой.

Для каждого угла построим смежный угол. Смежные углы — это два угла, у которых одна сторона общая, а две другие стороны образуют прямую линию, то есть сумма смежных углов равна \(180^\circ\).

Если задан угол \( \alpha \), то смежный к нему угол равен \(180^\circ — \alpha\).

Таким образом:

— Острый угол \( \alpha < 90^\circ \), смежный \( 180^\circ — \alpha > 90^\circ \) (тупой).
— Прямой угол \( 90^\circ \), смежный тоже \( 90^\circ \).
— Тупой угол \( \alpha > 90^\circ \), смежный \( 180^\circ — \alpha < 90^\circ \) (острый).

1) Начертим три угла, удовлетворяющих условию задачи: острый, прямой и тупой.

2) Смежные углы по определению являются двумя углами, у которых одна сторона общая, а две другие стороны являются дополнительными полупрямыми. Таким образом, вместе смежные углы составляют развёрнутый угол, равный \(180^\circ\). Отсюда следует, что для построения смежного угла достаточно построить развёрнутый угол от одной из сторон заданного угла.

3) Построим смежные углы к каждому из трёх углов. Если задан угол \( \alpha \), то смежный угол будет равен \(180^\circ — \alpha\).

Для острого угла \( \alpha < 90^\circ \) смежный угол будет тупым, так как \(180^\circ — \alpha > 90^\circ\).

Для прямого угла \( \alpha = 90^\circ \) смежный угол также равен \(90^\circ\).

Для тупого угла \( \alpha > 90^\circ \) смежный угол будет острым, так как \(180^\circ — \alpha < 90^\circ\).

Таким образом, построены три угла и к каждому из них — смежный угол, удовлетворяющие условию задачи.