ГДЗ по Геометрии 7 класс Номер 47 Атанасян — Подробные Ответы

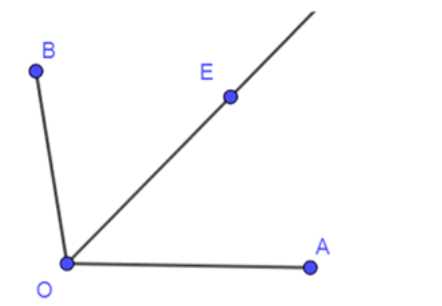
Луч ОЕ делит угол АОВ на два угла. Найдите угол АОВ, если:
а) угол АОЕ = 44°, угол ЕОВ = 77°;
б) угол АОЕ = 12°37′, угол ЕОВ = 108°25′.

Луч ОЕ делит угол АОВ на два угла: \(\angle AOE\) и \(\angle EOB\).

а) Чтобы найти \(\angle AOB\), складываем углы:
\[
\angle AOB = \angle AOE + \angle EOB = 44^\circ + 77^\circ = 121^\circ.
\]

б) Складываем углы с минутами:
\[
\angle AOB = 12^\circ 37′ + 108^\circ 25′ = (12 + 108)^\circ + (37′ + 25′) = 120^\circ 62′.
\]
Так как \(62′ = 1^\circ 2’\), то:
\[
\angle AOB = 121^\circ 2′.
\]

Ответ:
а) \(121^\circ\)
б) \(121^\circ 2’\)

1) Луч ОЕ делит угол АОВ на два угла — \(\angle AOE\) и \(\angle EOB\). Это значит, что угол АОВ можно найти, сложив величины этих двух углов. По определению смежных углов или углов, образованных лучами, сумма частей равна целому углу. Поэтому, если нам известны значения \(\angle AOE\) и \(\angle EOB\), мы можем получить величину \(\angle AOB\), сложив их.

2) а) В первом случае даны углы \(\angle AOE = 44^\circ\) и \(\angle EOB = 77^\circ\). Чтобы найти угол АОВ, складываем данные градусы:
\(\angle AOB = 44^\circ + 77^\circ\). При сложении целых чисел \(44 + 77 = 121\), следовательно, \(\angle AOB = 121^\circ\). Здесь не возникает необходимости в переводе минут, так как углы даны только в градусах. Итоговый угол — это сумма двух частей, что соответствует свойству угла, разделённого лучом.

3) б) Во втором случае углы заданы с минутами: \(\angle AOE = 12^\circ 37’\) и \(\angle EOB = 108^\circ 25’\). Для сложения таких углов необходимо отдельно сложить градусы и минуты. Сначала складываем градусы: \(12^\circ + 108^\circ = 120^\circ\). Затем складываем минуты: \(37′ + 25′ = 62’\). Поскольку в одном градусе 60 минут, 62 минуты — это больше одной единицы градуса. Переводим 62 минуты в градусы и минуты: \(62′ = 60′ + 2′ = 1^\circ + 2’\). Прибавляем 1 градус к сумме градусов: \(120^\circ + 1^\circ = 121^\circ\). Минуты остаются \(2’\). Таким образом, итоговый угол равен \(121^\circ 2’\). Это соответствует правилу сложения углов, учитывая перевод минут в градусы при превышении 60 минут.

Ответ:
а) \(121^\circ\)
б) \(121^\circ 2’\)