
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 342 Атанасян — Подробные Ответы
Докажите теорему: если в треугольнике биссектриса является медианой, то треугольник равнобедренный.
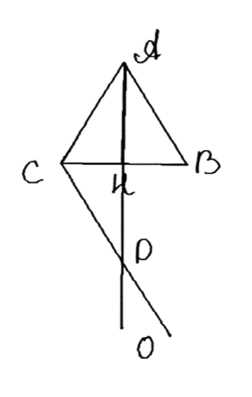
Дано: треугольник ABC, AM медиана и биссектриса. Требуется доказать, что треугольник ABC равнобедренный.
Биссектриса AM делит угол BAC на два равных угла, а также каждая точка на ней равноудалена от сторон угла. Следовательно, BM является серединным перпендикуляром к AC. Так как AM медиана, то AM = MC. Рассмотрим треугольники ABM и CBM. Они прямоугольные, имеют общий катет BM и равные катеты AM и MC. По признаку равенства прямоугольных треугольников следует, что AB = BC. Таким образом, треугольник ABC равнобедренный.
Дано: треугольник ABC, AM является одновременно медианой и биссектрисой. Требуется доказать, что треугольник ABC равнобедренный.
1. Рассмотрим свойство биссектрисы. Биссектриса угла делит его на два равных угла, и каждая точка на биссектрисе равноудалена от сторон этого угла. Следовательно, отрезок BM, проведённый перпендикулярно к стороне AC, является серединным перпендикуляром, то есть BM перпендикулярен AC.
2. По условию AM является медианой, а это значит, что точка M — середина отрезка AC. Следовательно, AM = MC.
3. Рассмотрим треугольники ABM и CBM. Эти треугольники являются прямоугольными, так как BM перпендикулярен AC. В этих треугольниках:
— катет BM общий для обоих треугольников,
— катеты AM и MC равны, так как AM = MC (по свойству медианы).
4. По признаку равенства прямоугольных треугольников (по двум катетам) треугольники ABM и CBM равны.
5. Из равенства треугольников ABM и CBM следует, что соответствующие стороны AB и BC равны.
6. Таким образом, стороны AB и BC равны, что доказывает, что треугольник ABC является равнобедренным.
Доказательство завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!