ГДЗ по Геометрии 7 класс Номер 337 Атанасян — Подробные Ответы

Внутри равнобедренного треугольника ABC с основанием ВС взята такая точка М, что ∠MBC = 30°, ∠MCB = 10°. Найдите угол АМС, если ∠BAC = 80°.

Треугольник ABC равнобедренный, AB = AC, угол BAC = 80°.

Углы при основании: ∠ABC = ∠ACB = (180° — 80°) / 2 = 50°. Проведем AD, которая является высотой, медианой и биссектрисой. Углы ∠CAD и ∠BAD равны по 40°. Рассмотрим треугольник AMC. Он равнобедренный, так как AC = CM. Угол ∠ACM = 40°. Углы при основании треугольника AMC равны: ∠CAM = ∠CMA = (180° — 40°) / 2 = 70°. Угол ∠AMC = 180° — ∠CAM — ∠CMA = 70°. Ответ: угол AMC равен 70°.

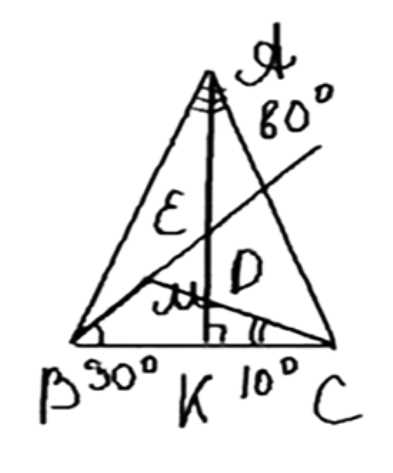
1. Рассмотрим треугольник ABC. Он равнобедренный, так как AB = AC. Угол BAC задан и равен 80°. Чтобы найти углы при основании (углы ABC и ACB), используем формулу для суммы углов треугольника:
∠ABC = ∠ACB = (180° — 80°) / 2 = 50°.

2. Проведем AD, которая является высотой, медианой и биссектрисой треугольника ABC. Это значит, что AD делит угол BAC пополам, а также делит сторону BC на два равных отрезка (BM = MC).

3. Рассмотрим треугольники AOC и AOB. У них общая сторона AO. Угол CAO равен углу BAO, так как AD — это биссектриса, а значит:
∠CAO = ∠BAO = 40°. Кроме того, AC = AB, так как треугольник ABC равнобедренный. По признаку равенства треугольников (две стороны и угол между ними) треугольники AOC и AOB равны. Следовательно:
∠AOC = ∠AOB,
∠ACO = ∠ABO.

4. Найдем угол ACO. Так как ∠ABC = 50°, а AD делит этот угол пополам, то:
∠ACO = ∠ABO = 50° — 30° = 20°.

5. Рассмотрим угол OCM. Угол OCM можно найти, вычитая из угла ACB (50°) углы ACO и MCB:
∠OCM = 50° — 20° — 10° = 20°.

6. Найдем угол AOC. Углы AOC и AOB равны, а сумма углов в треугольнике AOC равна 180°. Тогда:
∠AOC = ∠AOB = 180° — ∠ACO — ∠CAO = 180° — 20° — 40° = 120°.

7. Угол COB можно найти, используя сумму углов вокруг точки O. Сумма всех углов вокруг точки O составляет 360°, а углы AOC и AOB равны. Тогда:
∠COB = 360° — 2 × ∠AOC = 360° — 240° = 120°.

8. Рассмотрим треугольники ACO и COM. У них общая сторона CO. Углы COA и COM равны, так как угол AOC делится медианой AD пополам. Также углы ACO и CMO равны и равны 20°. По признаку равенства треугольников (сторона и два прилежащих угла) треугольники ACO и COM равны. Следовательно:
AC = CM.

9. Рассмотрим треугольник AMC. Угол AMC можно найти, используя сумму углов треугольника:
∠AMC = 180° — ∠ACM — ∠CAM.
Угол ACM равен 40°, а так как AC = CM (треугольник AMC равнобедренный), то ∠CAM = ∠CMA. Пусть ∠CAM = x. Тогда:
∠AMC = 180° — 40° — x = 140° — x.
Так как треугольник равнобедренный, то:
x = (180° — ∠AMC) / 2 = (180° — 140°) / 2 = 70°.

10. Подставим значение x в выражение для угла AMC:
∠AMC = 140° — x = 140° — 70° = 70°.

Ответ: угол AMC равен 70°.