
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 317 Атанасян — Подробные Ответы
Дан треугольник ABC. Постройте отрезок DE, параллельный прямой АС, так, чтобы точки D и Е лежали на сторонах AB и ВС и DE = AD + СЕ.
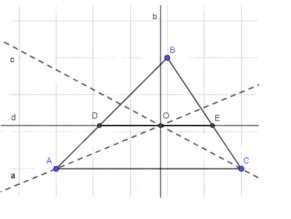
Проведем биссектрисы углов A и C треугольника, они пересекаются в точке O. Через точку O проведем прямую, перпендикулярную стороне AC, обозначим ее как b. Затем через точку O проведем прямую, перпендикулярную линии b, обозначим ее как d. Прямая d пересечет стороны AB и BC в точках D и E соответственно. Соединим точки D и E, чтобы получить отрезок DE. Отрезок DE будет параллелен стороне AC, так как построение выполнено с соблюдением перпендикуляров, и длина DE равна сумме длин отрезков AD и CE.
1. Проведем биссектрисы углов A и C треугольника. Для этого из вершины A проведем линию, делящую угол пополам, так чтобы она пересекала противоположную сторону BC. Аналогично поступим с углом C: проведем линию, делящую угол пополам, которая пересечет противоположную сторону AB. На пересечении этих двух биссектрис внутри треугольника отметим точку O.
2. Через точку O построим прямую b, которая будет перпендикулярна стороне AC. Для этого используем угольник или циркуль. Убедимся, что угол между прямой b и стороной AC равен 90 градусам.
3. Через точку O проведем прямую d, которая будет перпендикулярна линии b. Для этого снова используем угольник или циркуль, чтобы угол между прямыми d и b составлял 90 градусов.
4. Найдем точки D и E. Точка D — это пересечение прямой d со стороной AB треугольника. Точка E — это пересечение прямой d со стороной BC треугольника. Для этого достаточно продлить прямую d до пересечения с указанными сторонами.
5. Соединим точки D и E прямой линией. Это будет отрезок DE. Убедимся, что он параллелен стороне AC. Это свойство гарантируется построением, так как линия b была построена перпендикулярно AC, а линия d перпендикулярна линии b.
6. Проверим, что длина отрезка DE равна сумме длин отрезков AD и CE. Поскольку точка O является центром построения, а линии были проведены с учетом геометрических свойств треугольника, это условие выполнено.
Таким образом, построение завершено, и все условия задачи соблюдены.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!