
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 302 Атанасян — Подробные Ответы
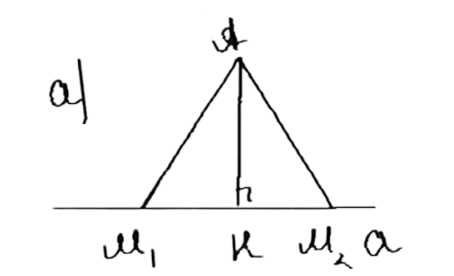
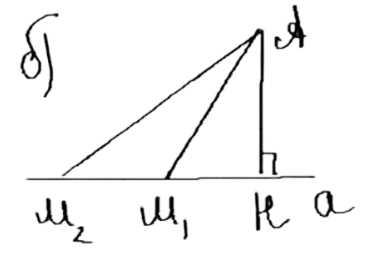
Из точки А к прямой a проведены перпендикуляр АН и наклонные АМ1 и АМ2. Докажите, что:
а) если АМ1 = АМ2, то НМ1 = НМ2;
б) если АМ1 < АМ2, то HM1 < HM2.
а) Рассмотрим треугольники AM1H и AM2H. Они прямоугольные, так как AH перпендикулярно прямой a. У них общий катет AH, углы при основании равны 90 градусов, а гипотенузы AM1 и AM2 равны по условию. Следовательно, треугольники равны по двум катетам, что означает равенство оставшихся сторон: HM1 = HM2.
б) Рассмотрим треугольники AM1H и AM2H. Они прямоугольные, так как AH перпендикулярно прямой a. По теореме Пифагора HM1 = √(AM1² — AH²), а HM2 = √(AM2² — AH²). Так как AM1 < AM2, то AM1² < AM2², следовательно, HM1 < HM2.
а) Рассмотрим треугольники AM1H и AM2H. Эти треугольники являются прямоугольными, так как AH перпендикулярно прямой a. У данных треугольников общий катет AH. Углы при основании H равны 90 градусов, так как AH — перпендикуляр к прямой a. По условию задачи гипотенузы AM1 и AM2 равны, то есть AM1 = AM2.
Согласно признаку равенства прямоугольных треугольников, если два катета одного треугольника равны двум катетам другого треугольника, то такие треугольники равны. В данном случае треугольники AM1H и AM2H равны по двум катетам: AH — общий катет, а AM1 = AM2 по условию задачи. Из равенства треугольников следует равенство всех соответствующих сторон, то есть HM1 = HM2. Таким образом, доказано, что если AM1 = AM2, то HM1 = HM2.
б) Рассмотрим треугольники AM1H и AM2H. Они являются прямоугольными, так как AH перпендикулярно прямой a. Применим теорему Пифагора для нахождения длин катетов HM1 и HM2. Для треугольника AM1H имеем: HM1 = √(AM1² — AH²). Для треугольника AM2H имеем: HM2 = √(AM2² — AH²).
По условию задачи AM1 < AM2. Это означает, что AM1² < AM2². Так как AH² является одинаковым для обоих выражений, то разность AM1² — AH² будет меньше, чем разность AM2² — AH². Следовательно, √(AM1² — AH²) < √(AM2² — AH²), то есть HM1 < HM2. Таким образом, доказано, что если AM1 < AM2, то HM1 < HM2.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!