
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7-9 класс Номер 3 Атанасян — Подробные Ответы
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Пусть даны три прямые: \(a\), \(b\), \(c\).
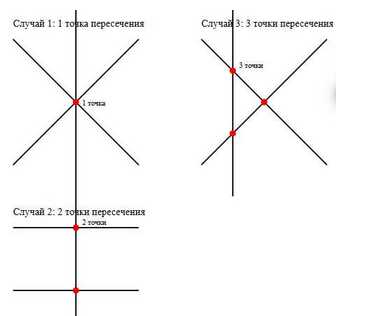
1. Если все три прямые пересекаются в одной точке, то есть \(a \cap b = b \cap c = a \cap c = P\), то количество точек пересечения равно 1.
2. Если две прямые параллельны, например \(a \parallel b\), а третья \(c\) пересекает их, то точки пересечения будут \(a \cap c = P\) и \(b \cap c = Q\), всего 2 точки.
3. Если все три прямые пересекаются попарно в разных точках, то есть \(a \cap b = P\), \(b \cap c = Q\), \(a \cap c = R\), то всего 3 точки пересечения.
Итого возможные варианты:
| Случай | Количество точек пересечения |
|---|---|
| 1. Три прямые пересекаются в одной точке | 1 |
| 2. Две прямые параллельны, третья пересекает их | 2 |
| 3. Три прямые пересекаются попарно | 3 |
1. Рассмотрим три прямые \(a\), \(b\), \(c\). Пусть все три прямые пересекаются в одной точке \(P\). Это значит, что точки пересечения пар прямых совпадают: \(a \cap b = b \cap c = a \cap c = P\). В этом случае количество точек пересечения равно 1, так как все три пересечения — одна и та же точка.
2. Теперь предположим, что две прямые параллельны, например \(a \parallel b\), а третья прямая \(c\) пересекает их. Тогда прямая \(c\) пересечёт прямую \(a\) в точке \(P\) и прямую \(b\) в точке \(Q\). Поскольку \(a\) и \(b\) не пересекаются, точки пересечения будут только эти две: \(a \cap c = P\) и \(b \cap c = Q\). Следовательно, количество точек пересечения равно 2.
3. Рассмотрим случай, когда все три прямые пересекаются попарно в разных точках. Это значит, что каждая пара прямых имеет свою точку пересечения: \(a \cap b = P\), \(b \cap c = Q\), \(a \cap c = R\), и все точки \(P\), \(Q\), \(R\) различны. В таком случае общее количество точек пересечения равно 3.
Итог:
| Случай | Количество точек пересечения |
|---|---|
| 1. Три прямые пересекаются в одной точке | 1 |
| 2. Две прямые параллельны, третья пересекает их | 2 |
| 3. Три прямые пересекаются попарно | 3 |
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!